Дробные факторные планы испытаний. Планирование испытаний

Рассмотрим порядок статистического анализа результатов испытаний. Для проверки условия воспроизводимости по формуле (11) определим

; ; ; .

Затем вычислим расчетное значение статистики критерия Кохрена:

.

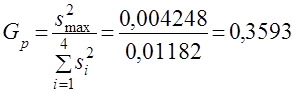При уровне значимости и числе степеней свободы , находим . Поскольку , принимается гипотеза об однородности данных (воспроизводимости результатов испытаний). Следовательно, дисперсия испытаний может быть определена по всем испытаниям согласно зависимости (12):

.

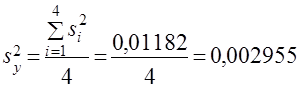Из (9) видно, что погрешность оценивания

.

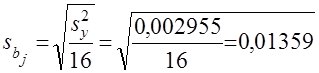Для проверки значимости коэффициентов и уточнения вида модели вычислим расчетные значения статистики -критерия по формуле (13):

; ; .

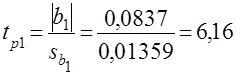Из таблицы Приложения при и получим . Следовательно, для и имеет место и эти коэффициенты значимо отличаются от нуля. Поскольку коэффициент оказался незначимым. Поэтому фактор из дальнейшего рассмотрения исключаем. Уточненная модель принимает вид

.

Для проверки адекватности модели определим предсказанные этой моделью значения ; ; ; . Согласно зависимости (14) мера неадекватности модели оценивается дисперсией

.

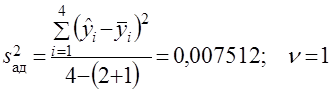Тогда определяемое по (15) расчетное значение статистики критерия

.

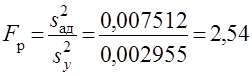При , , находим , что позволяет принять гипотезу об адекватности модели изучаемому процессу и использовать ее в дальнейшем для настройки двигателя.

Если целью испытаний является изучение характера процесса, то с получением адекватной модели они могут быть завершены. При доводочных испытаниях, когда – параметры конструкции, работа продолжается для получения координат точки в которой соответствует заданному (или экстремальному) значению. Рассмотрим два основных подхода к отысканию области оптимума : крутое восхождение и симплексный метод.

Крутое восхождение (метод Бокса-Уилсона) выгодно отличается от традиционной организации многофакторного эксперимента, при проведении которого последовательно отыскивается экстремум по каждому из факторов. Сущность крутого восхождения заключается в шаговом движении в направлении наибольшего изменения функции (направлении градиента)

Актуально о образовании:

Связь цели и содержания воспитания
Цели воспитания - это ожидаемые изменения в человеке (или группе людей), осуществленные под воздействием специально подготовленных и планомерно проведенных воспитательных акций и действий. Процесс формулировки таких целей, как правило, аккумулирует гуманистическое отношение воспитателя (группы или ...

Особенности физического воспитания детей старшего дошкольного возраста в ДОУ
Физическое воспитание детей - одна из ведущих задач дошкольных учреждений. Здоровье, полученное в дошкольном возрасте, является фундаментом общего развития человека. При этом понятие "здоровье" поднимает роль физической культуры на совершенно новый уровень, становясь основой формирования ...

Методика формирования пространственного образа на уроках геометрии
Одним из основных условий формирования пространственных представлений в процессе обучения геометрии является использование упражнений, ориентированных на формирование и развитие комплекса умений, составляющих содержание пространственных представлений и характеризующих их сформированность. Но не все ...