Дробные факторные планы испытаний. Планирование испытаний

Пусть для получения линейной модели реализован ПФП . Согласно рис. 1,б экспериментальные точки лежат в вершинах куба. Если линейная модель неадекватна, то в план включается так называемых «звездных точек» с координатами , расположенных на сфере диаметром (рис. 3). Таким образом, каждая из точек плана лежит на координатных осях на расстоянии от центра плана, называемым звездным плечом . Центром плана является центральная точка прямоугольника, если число факторов , куба при , гиперкуба, когда . Наличие звездных точек, собственно, и задает центральный композиционный план.

Представление о положении звездных точек в факторном пространстве дают следующие примеры: при и ядре плана, образованном ПФП , величина звездного плеча ; если , а в ядре реализован ПФП , то ; при и ПФП . Общее число испытаний при реализации ЦКП

,

где – ядро плана, – число звездных точек; – количество испытаний, проводимых в центре плана.

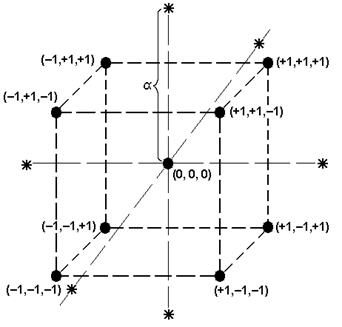
Рис. 3. «Звездные точки» с координатами

Пример ЦКП, в котором сохранено свойство ортогональности, приведен в табл. 11. В этом плане , , .

Поскольку в ЦКП ортогональность обеспечивается, оценки коэффициентов получаются независимо. Однако дисперсии , как видно из приводимой расчетной зависимости, неодинаковы для разных коэффициентов:

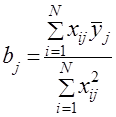; (19)

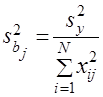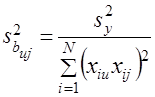; . (20)

Таблица 11

Актуально о образовании:

Обзор средств Интернет для формирования исследовательской компетенции на уроках английского языка
В параграфе 1.3 нами были рассмотрены основные виды Интернет-технологий, которые можно использовать в процессе обучения английскому языку для формирования исследовательской компетенции старшеклассников. В данном параграфе мы рассмотрим конкретные Интернет-ресурсы для развития исследовательских умен ...

Связь и различие эстетического и художественного воспитания и образования
Для отечественной педагогической мысли характерна постановка проблемы формирования и развития эстетического потенциала личности. Уже в 1890 году русский педагог В.П.Острогорский в "Письмах об эстетическом воспитании" обращал, внимание на то, что в школе необходимо не только формально разв ...

Особенности лексической стороны речи у детей со стертой дизартрией
В предыдущих главах нашего исследования мы рассмотрели онтогенез лексической системы при нормальном речевом развитии ребенка. Однако под влиянием различные неблагоприятных воздействий, как во внутриутробном периоде развития, так и во время родов, а так же в первые годы жизни ребенка могут приводить ...