Дробные факторные планы испытаний. Планирование испытаний

Для проверки гипотезы можно воспользоваться критериями Кохрена или Бартлетта. Если , расчетное значение статистики критерия Кохрена определяется по формуле и гипотеза принимается, если , где , . Если дисперсии однородны (принята гипотеза ), то дисперсия опыта (или, что то же самое, дисперсия воспроизводимости) подсчитывается по зависимости

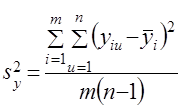, (11)

где знаменатель характеризует число степеней свободы . В общем случае, подсчитывается как среднее взвешенное значение

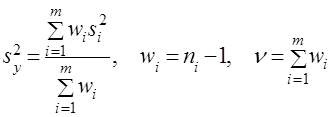. (12)

Проверка значимости коэффициентов регрессии позволяет лучше осмыслить математическое описание процесса, а также уточнить вид модели путем отсеивания факторов, слабо влияющих на значение выходного параметра. Проверка значимости каждого из коэффициентов производится независимо, с помощью проверки гипотезы 0 по -критерию. Расчетные значения статистики критерия можно определить по соотношению

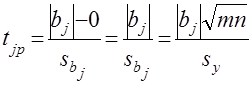. (13)

Если , то коэффициент является значимым и соответствующий фактор оказывает существенное влияние на величину . Статистическая незначимость может быть вызвана следующими причинами:

интервал варьирования был выбран слишком малым;

уровень начального режима по фактору оказался близок к точке частного экстремума ;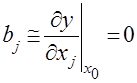

велика ошибка опыта из-за влияния неуправляемых и неконтролируемых факторов;

данный фактор (совокупность факторов) не оказывают заметного влияния на величину выходного параметра.

Поскольку план ортогонален и коэффициенты оцениваются независимо друг от друга, оказавшиеся незначимыми коэффициенты могут быть отброшены без пересчета остальных.

Проверка адекватности заключается в подтверждении предположения, что полученная математическая модель достаточно верно описывает характер процесса. Формальное содержание гипотезы состоит в том, что предсказанные уравнением (расчетные) значения выходного параметра отклоняются от опытных на величину, не превышающую некоторый наперед заданный уровень, и модель пригодна для обоснования инженерных решений. Для проверки гипотезы оценивается дисперсия адекватности

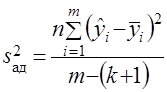; . (14)

Если дисперсия адекватности не превышает дисперсии опыта , то есть основание полагать, что модель адекватно описывает процесс. Согласно п. 1.3 для проверки гипотезы о дисперсиях используется -критерий. Статистика критерия

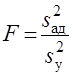. (15)

Модель считается адекватной процессу, если , где , . Если ,то для получения адекватного описания необходимо увеличить порядок аппроксимирующего полинома. Очевидно, что проверка адекватности возможна лишь в том случае, если , то есть число разных испытаний превосходит количество включаемых в модель факторов.

Актуально о образовании:

Морфологический анализ
Морфологический анализ (метод морфологического анализа) — основан на подборе возможных решений для отдельных частей задачи и последующем систематизированном получении их сочетаний (комбинировании). Относится к эвристическим методам. Метод разработан швейцарским астрономом Фрицем Цвикки. Благодаря э ...

Исследование составляющей когнитивного развития учеников – мышления и его связей с учебными достижениями по математике
С целью установления связей между характеристиками мышления и учебными достижениями по математике было проведено исследование в ОМК. Исследование проводилось в октябре – ноябре 2011 года, в котором были задействованы учащиеся 7-го класса (всего 13 человек). Исследование проводилось в двух направлен ...

Качества личности творческого педагога
В широком понимании творческой индивидуальностью можно считать человека, который обладает сформировавшимся цельным ядром личности, богатым внутренним миром, обусловливающими черты характера и выражающимися в автономности, активности, своеобразии и оригинальности всех проявлений личности, в творческ ...