Дробные факторные планы испытаний. Планирование испытаний

В дальнейшем проведение реальных испытаний чередовалось с мысленными опытами. При подсчете предсказанных значений натуральные значения переводились в кодированные по формуле. Как видно из табл. 2.11, переход от условий испытаний № 5 к условиям испытания № 6 не обеспечивает приращения удельной тяги. Далее в точке (рис. 3.2) была проведена контрольная серия из четырех испытаний, которая подтвердила, что дальнейшие вариации и не ведут к увеличению .

Симплексный метод заключается в том, что испытания проводятся в точках факторного пространства, соответствующих вершинам симплексов. Под -мерным симплексом подразумевают выпуклую геометрическую фигуру, имеющую вершину, соединенные прямыми отрезками-ребрами. Одномерным симплексом будет отрезок прямой, двумерным – плоский треугольник, трехмерным – тетраэдр и т.д. При планировании испытаний обычно используют правильные симплексы, у которых вершины находятся друг от друга на одинаковом расстоянии. В отличие от крутого восхождения, при использовании симплексного метода процесс изучения поверхности отклика совмещается с движением к экстремуму. Схема поиска экстремума симплекс-методом при показана на рис. 2. Сначала проводится серия испытаний в вершинах правильного -мерного симплекса (точки ) с целью выявить точку, характеризующую условия, при которых получаются худшие результаты. Следующую серию испытаний проводят в вершинах нового симплекса, который получают заменой точки, соответствующей худшему результату (точка ), ее зеркальным отображением. Тем самым достигается смещение центра тяжести симплекса в направлении экстремума. В дальнейшем процедура повторяется, и образуется последовательность симплексов, перемещающихся в факторном пространстве в направлении к экстремуму. На близость экстремума указывает начинающееся вращение симплекса вокруг одной из его вершин.

Шаговое движение к экстремуму продолжается до тех пор, пока будет достигнута «почти стационарная область», которая не может быть описана линейной моделью, и где значимы совместные (квадратичные) эффекты воздействия.

Близость «почти стационарной области» можно установить, если провести серию испытаний в центре плана и определить значение выходного параметра . Вычисляемое для линейной модели значение при реализации ПФП или ДФП в «почти стационарной области» является совместной оценкой для свободного члена и суммы квадратов членов. Следовательно, разность дает представление о кривизне поверхности отклика.

«Почти стационарную область» в большинстве случаев с приемлемой точностью можно описать уравнением второго порядка

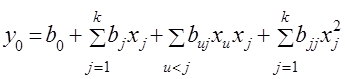. (18)

Поскольку для отыскания раздельных оценок параметров число уровней должно быть на единицу больше степени полинома, число уровней должно быть не менее трех. Однако применение ПФП типа приведет к резкому возрастанию количества испытаний. Для сокращения можно использовать центральные композиционные планы (ЦКП). Ядро ЦКП составляют ПФП или ДФП: ПФП, если число факторов , и ДФП при . Это приводит к тому, что если после реализации ПФП (ДФП) гипотеза о линейности модели не подтвердилась, нет необходимости проводить испытания заново. Для получения модели второго порядка достаточно добавить к ПФП (ДФП) несколько специальным образом подобранных точек, в которых и провести дополнительную серию испытаний.

Актуально о образовании:

Ознакомление детей 7 лет с немецкой культурой
1. развитие коммуникативных навыков у детей, творческой активности и самостоятельности. 2. расширение представлений о культуре, традициях, праздниках в Германии. 3. развитие творческих, художественных, актёрских способностей. 4. вызвать у детей желание участвовать в коллективной деятельности. Работ ...

Основные направления деятельности студента-практиканта
(Фамилия, имя, отчество) _ № п/п Вид деятельности Содержание деятельности Отметка о выполнении Ознакомительная Знакомство с коллективом, детьми, с методическими требованиями и т.д. Знакомство с личными делами и медицинскими картами учащихся. Составление индивидуального плана работы на весь период п ...

ПК как средство обучения
Последние технические достижения часто находили применение в учебном процессе, и ПК в этом смысле не является исключением. Уже первые опыты применения ПК в учебном процессе показали, что использование вычислительной техники позволяет существенно повысить эффективность процесса обучения, улучшить уч ...