Дробные факторные планы испытаний. Планирование испытаний

Принцип проверки статистических гипотез состоит в том, что если расчетное значение попадает в область допустимых значений, то принимают гипотезу . При попадании в критическую область отвергается и принимается гипотеза . Заметим, что принятие не означает, что доказана ее справедливость, а свидетельствует лишь о том, что результаты испытаний выборки не противоречат выдвинутым предположениям о свойствах объекта (генеральной совокупности). Необходимо иметь в виду, что продолжение испытаний может привести к иному заключению.

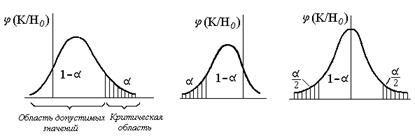
Рис. 1. Область допустимых значений и критическая область

Таким образом, правильное определение вида критической области и уровня значимости наряду с выбором статистики критерия; в основном, определяют достоверность статистического решения. В основе выбора лежит анализ последствий совершения ошибки первого или второго рода, поскольку одновременно уменьшить и невозможно. Для случая правосторонней критической области это иллюстрируется рис. 2. Если смещать вправо [не изменяя положения кривых ], то с уменьшением мощность критерия снижается. Если переместить влево, увеличивается, зато возрастает мощность критерия. Формализованные методы установления критической области основываются на том, что величины и связаны с объемом испытаний .

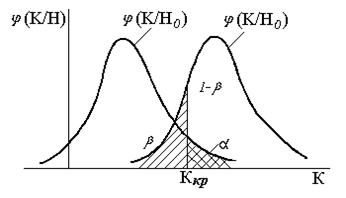
Рис. 2. Случай правосторонней критической области

Если выбрана, то при фиксированном можно руководствоваться критерием Неймана-Пирсона, в соответствии с которым из всех областей фиксированного уровня в качестве критической выбирается наиболее мощная (обеспечивающая максимум величины ). Увеличение (возрастание затрат на испытание) является единственным способом одновременного снижения и . Интуитивно значения выбираются в диапазоне . При проверке гипотез относительно технических характеристик ракет, агрегатов наземного оборудования, артиллерийских комплексов . Оценивая показатели качества (надежности, эффективности), область допустимых значений целесообразно расширить (). Более жесткие условия могут задаваться при проверке однородности характеристик контрольно-испытательной аппаратуры и свойств элементов, испытываемых в лабораторных условиях .

2. Проверка гипотез о параметрах

Рассмотрим первую группу задач статистической проверки гипотез, обеспечивающих принятие решений о средних значениях параметров. Возможны две основные задачи: проверка соответствия математических ожиданий одноименных параметров (задача проверки однородности), проверка соответствия этих математических ожиданий требованиям ТТЗ (ТУ).

Актуально о образовании:

Взаимодействие телевидения и современной школы
Человек XXI века живет в медиа-пространстве, которое составляет его новую среду обитания, реальность современной культуры. Средства массовой коммуникации проникли во все сферы жизни. Медиа стали основным средством производства современной культуры, а не только передаточным механизмом. Информационны ...

Система работы по развитию творческих способностей на формирующем этапе эксперимента
Задачи экспериментальной работы: -исследование воздействия эстетических качеств среды на физиологию, психику, интеллект младших школьников; -организация эстетико-педагогических условий в учебно-воспитательной деятельности на протяжении формирующего эксперимента; -организация творческой деятельности ...

Творческие находки учителей технологии в создании увлекательных уроков: анализ практической деятельности
Три основных вопроса каждодневно встают перед учителем при подготовке к занятиям: Для чего учить? Чему учить? Как учить? Программы, учебники, методические пособия существенно помогают ему при решении первых двух вопросов. Правда и тут он многое должен додумать сам, учитывая конкретные задачи обучен ...