Приемы работы по повышению умений и навыков решать текстовые задачи младшими школьниками

В рамках формирующего этапа эксперимента нами были проведен в экспериментальном классе цикл уроков по математике. Система работы и подобранные задания были направлены на оптимизацию процесса обучения по формированию умений у младших школьников решать текстовые задачи, а именно предполагало выработать:

умение выделять структурные элементы в текстовой задаче;

умение анализировать задачу;

умение проводить поиск плана решения задачи;

умение реализовать найденный план решения задачи;

умение осуществлять контроль и коррекцию решения.

Чтобы научить школьника работе над текстовой задачей, учитель может использовать различные приемы, методы обучения, соответствующие совершенствованию логического мышления и творческих способностей детей. Раскроем фрагменты уроков, на которых мы применяли данные задания.

Фрагмент урока №1

Цель урока: научить школьников составлять задачу по данной схеме, сформировать умение выделять структурные элементы в текстовой задаче.

На доске вывешиваются схемы. Мы предлагаем учащимся составить по данной схеме задачу, а затем решить ее.

Задача №1

Учащиеся составляют задачу по схеме:

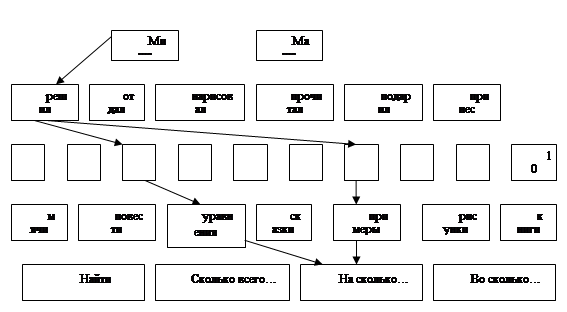
Рис.3.2.1 Схема для составления текстовой задачи

"Миша решил 3 уравнения и 7 примеров. На сколько больше примеров, чем уравнений, решил Миша? На сколько меньше уравнений, чем примеров, решил Миша?"

Решение:

7 - 3 = 4 (шт.)

Ответ: на 4 примера больше, чем уравнений, решил Миша.

Задача №2

Алогичная работа проводится со следующей схемой (Рис.3.2.2.).

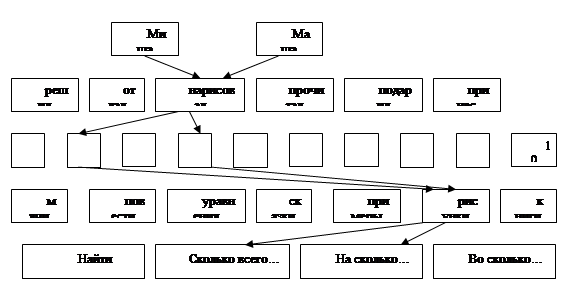
Рис.3.2.2 Схема для составления текстовой задачи

"Миша нарисовал 2 рисунка, а Маша 4. Сколько всего рисунков нарисовали дети? На сколько рисунков больше

нарисовала Маша, чем Миша?"

Решение:

2 + 4 = 6 (шт.) - нарисовали вместе.

4 - 2 = 2 (шт.) - Маша нарисовала больше Миши.

Ответ: 6 рисунков, на 2 рисунка.

Фрагмент урока №2

Цель урока: научить школьников соотносить реальную ситуацию с ее математической моделью, сформировать умение анализировать задачу.

Задача №1

На доске заранее вывешиваются карточки с объектами "овощи", "свекла", "морковь", "картофель", а также вспомогательная модель задачи.

Учащимся дают следующие команды:

Выберите слова, характеризующие сюжет задачи. (Школьники вырастили овощи.)

Где выращивают школьники овощи? (На пришкольном участке).

Какое слово из предложенных объектов, записанных в столбце, общее? (Овощи.)

Соотнесите предложенные объекты со схемой, указав количественные характеристики. (Целое - овощи. Количество овощей неизвестно. Части: свекла - 20 кг, морковь - 12 кг, картофель - 8 кг).

Сформулируйте текст задачи. (Школьники вырастили на пришкольном участке 20 кг свеклы, 12 кг моркови и 8 кг картофеля. Сколько килограммов овощей вырастили школьники?)

О какой величине говорится в задаче? (О массе.)

Как иначе можно сформулировать требование? (Какова масса собранного урожая?)

Далее мы предлагаем ученикам самостоятельно решить эту задачу в рабочих тетрадях.

20 + 12 + 8 = 40 (кг)

Ответ: 40 кг урожая собрали школьники.

Затем совместно с школьниками проверяем правильность решения предложенной задачи. В качестве способа проверки могут выступать сравнение своего решения с выполненным на закрытой части доски, чтение решения вслух Прием составления задачи по предложенной программе действий. Данный прием развивает коммуникативные способности ребенка, способность неординарно мыслить, и рассчитан на учащихся не младше второго класса.

Актуально о образовании:

ПК как средство обучения
Последние технические достижения часто находили применение в учебном процессе, и ПК в этом смысле не является исключением. Уже первые опыты применения ПК в учебном процессе показали, что использование вычислительной техники позволяет существенно повысить эффективность процесса обучения, улучшить уч ...

Приемы развития творческих способностей младших школьников
Как развивать творческие способности ребенка? Как сделать его творческой личностью? Еще недавно эти вопросы педагогика перед собой не ставила. Школа готовила исполнителей, и это почти всех устраивало. А между тем проблемой развития творческих способностей люди интересовались всегда. Сегодня в решен ...

Особенности усвоения таблицы умножения в начальной школе
Рассмотрим принцип изучения таблицы умножения в системе Д.Б. Эльконина-В.В. Давыдова По мнению В.В. Давыдова, умножение является центральной темой программы 3 класса. Умножение в курсе 3 класса рассматривается как особое действие, связанное с переходом к новым меркам в процессе измерения величин. П ...