Что понимается под названием вычислительный эксперимент

Оператор 12 представляет собой счетчик числа обслуженных заявок, после каждой обслуженной заявки показание счетчика увеличивается на единицу.

С оператора 12 управление передается на оператор 7 и дальше формируется следующая заявка так же, как и в рассмотрением случае отказа в обслуживании.

Если неравенство не выполняется (следовательно , это означает, что -я заявка уже не принадлежит заданному интервалу, и реализация на этом заканчивается.

Оператор 13 представляет собой счетчик числа испытаний.

Оператор 14 проверяет, получено ли уже заданное число испытаний . Если неравенство выполняется, управление передается оператору 15.

Оператор 15 осуществляет подготовку к следующему испытанию. При этом очищаются рабочие ячейки, хранящие значения и , а содержимое ячеек, хранящих число отказов и обслуженных заявок, пересылаются в специальный массив для последующей статистической обработки. Дальше управление передается на оператор 3, и начинается очередное испытание.

Если неравенство не выполняется, управление передается оператору 16.

Оператор 16 осуществляет статистическую обработку полученных результатов и вычисляет требуемые показатели эффективности функционирования системы за время .

Можно моделировать работу системы за целый месяц в течение нескольких минут машинного времени. Преимущество «сжатия времени» при моделировании становится очевидным, если попытаться получить такую же информацию, используя физическую систему.

Пример. Рассмотрим, как можно моделировать однофазные системы обслуживания с помощью ручных вычислений. Этот пример должен пояснить основные идеи, описанные выше.

Пусть мы хотим моделировать систему массового обслуживания, поступление требований в которой подчинено пуассоновскому распределению со средним 3 клиента в час, а время обслуживания равно 0,2 ч с вероятностью 0,5 или 0,6 ч с вероятностью 0,5. Клиенты обслуживаются согласно дисциплине «первым пришел – первым обслуживаешься»; длина очереди, а также источник поступления клиентов не ограничены. Предположим, что в начальный момент моделирования клиентов нет.

Для пуассоновского входного потока со средней интенсивностью клиента в час промежутки времени между требованиями имеют экспоненциальное распределение и, как показано ранее, могут быть получены из формулы

.

Поскольку время обслуживания равно либо 0,2, либо 0,6 ч с равными вероятностями, время обслуживания определяется как

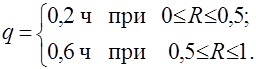
Актуально о образовании:

Роль проблемного обучения и его сущность
В данном параграфе мы проследим путь развития проблемного обучения в педагогической теории и практике отечественных и зарубежных педагогов. Еще с древних времен величайшие педагоги всегда искали методические пути преобразования учебного труда в радостный процесс мира, развития умственных сил и спос ...

Задачи на взвешивание и переливание
Данное занятие предлагается провести в виде практического занятия. Разбить класс на 2 группы. Каждой из групп предложить по задаче на взвешивание и переливание, после чего команда должна рассказать (показать) решение. Для следующих задач необходимо заранее подготовить сосуды емкостью 300мл, 400мл, ...

Наблюдение за птицами
Птичье население любой местности состоит из оседлых и прилетных видов. К оседлым относятся птицы, круглый год встречающиеся в данной местности, к прилетным - появляющиеся здесь на определенное время года. Большую часть последних в Свердловской области составляют виды, прилетающие весной на период г ...