Модифицированный имитационным моделированием метод экспоненциального сглаживания

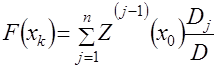, (4.35)

где – степенной определитель -го порядка (4.29), значение которого вычисляется методом перекрестного умножения (блоки 19, 20);

– определитель, получаемый из (4.29) заменой -й строки на функции – блок 23;

– вычисленная ранее производная.

Значение функции в каждой точке и ее отклонения вычисляются в блоках 21, 22, 24-26. При подстановке значений , и зависимость (4.35) принимает вид суперпозиции экспоненциальных законов, параметрами которых являются аргументы прогнозирующих зависимостей.

Если все корни комплексные, то имеет вид

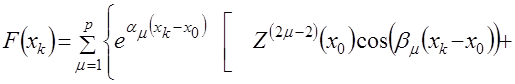
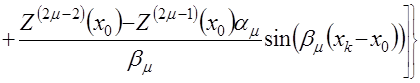,(4.36)

где – нечетное натуральное число;

– действительная часть корня; ; .

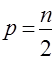Значения функции и ее отклонения вычисляются в блоках 28, 29. Если в результате анализа устанавливается, что корней комплексные, а корней действительные, то принимает вид

,

где вычисляется по зависимости (4.36) с использованием корней блок 38); при вычисляется по зависимости (4.35) с использованием корней (блоки 33, 34, 35, 41), при – в соответствии с блоками 32, 39, 40. Значения функции и ее отклонения от вычисляются в блоках 36, 37, 42, 43, 44. Результаты расчетов выводятся на печать. После вычисления функции и в каждом из приведенных случаев выбирается максимальное значение отклонения , которое сравнивается с заданным (блоки 45, 47).

Актуально о образовании:

Лингвопсихологический анализ письменной речи
В результате обучения иностранным языкам в средней школе учащиеся должны научиться не только говорить, но и читать и понимать иностранный текст. Чтение на иностранном языке является одной из целей обучения в средней школе. Чтение рассматривается как речевая деятельность, направленная на восприятие ...

Констатирующий этап эксперимента: описание диагностических методик по определению уровня творческих способностей младших школьников
Следующим этапом нашей работы был сбор сведений об уровне развития творческих способностей младших школьников. Мы сделали это, опираясь на данные, полученные в ходе работы с ученическим коллективом 1 класса средней школы №44 г. Краснодара. Детям предлагался ряд заданий, которые будут описаны ниже, ...

Подготовка учителя к организации развития творческого потенциала учащихся на уроках по культурологическим дисциплинам
Развитие творческого потенциала учащихся требует создания специальных условий познавательного учебного процесса. Успешное выполнение этих задач во многом зависит от понимания себя и самооценки учителя. Самопознание, самоуправление, забота о своем психическом здоровье – важнейшая задача любого педаг ...