Модифицированный имитационным моделированием метод экспоненциального сглаживания

Известно что любой процесс можно представить в

, (4.17)

где – исходный процесс (функция одного переменного);

– приближенная модель процесса (описание с помощью ФГС);

– остаток (некоторая функция точности приближения).

В наиболее общем виде ФГС для одного аргумента записывается в виде [1], [2]

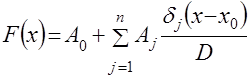, (4.18)

где – некоторое фиксированное натуральное число;

– начальное значение фактора-аргумента на рассматриваемом интервале;

– постоянные действительные параметры;

– специальный (степенной) определитель -го порядка;

– функция, получаемая из определителя заменой строки на соответствующие функции

, .

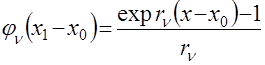При функция с гибкой структурой имеет вид

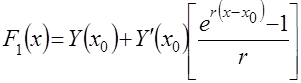, (4.19)

где – начальное значение функции и ее производной в точке ; – корень специального уравнения , в рассматриваемом случае .

Нахождение параметров функции связано с минимизацией базисной функции

. (4.20)

Далее представляется логичным определить порядок расчета параметров ФГС. В том случае, когда имеется всего один фактор, базисная функция имеет вид

. (4.21)

При на рассматриваемом отрезке функция равна нулю, и если проинтегрировать выражение (2.4.21) для того, чтобы избавиться от производных, можно получить

. (4.22)

Подставляя в это уравнение значение начальной точки, легко установить, что величина первой производной связана со значением величины и соотношением . (4.23)

Если проинтегрировать уравнение (22) еще раз, то можно записать выражение вида

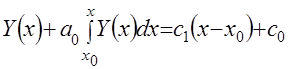. (4.24)

При условии, что , определяется . Тогда уравнение (4.24) целесообразно представить следующей зависимостью:

Актуально о образовании:

Проведение экспериментов, их анализ и обоснование
Тема работы, мы считаем очень серьезная, сложная, интересная и нужная. Нами использовано много методической литературы по этике. Практическая работа курсовой построена на экспериментах, которые оформлены в таблицы. Было проведено три эксперимента: констатирующий, формирующий и итоговый. Работая с у ...

Просветительские реформы Петра I
XVIIIвек для России – век кардинальных преобразований, подготовленным всем предшествующим ходом исторического развития – это период развития русской культуры, означавший постепенный переход от древнерусской культуры к культуре Нового времени (русской классической культуре XIXв.), начало которому по ...

Планы-конспекты уроков химии с применением технологии «французских мастерских»
Тема: Химические свойства алканов. Объект исследования: Химические свойства алканов. Реакции окисления. Реакции замещения. Получение и применение алканов. Цель: Развивать умения работать в парах и группах, развивать творческие способности. Развивать навыки самостоятельной работы и самоанализа. Иссл ...