Модифицированный имитационным моделированием метод экспоненциального сглаживания
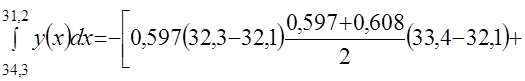
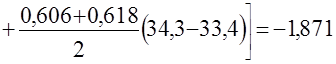 .
.
Значение интеграла 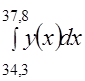 будет
будет
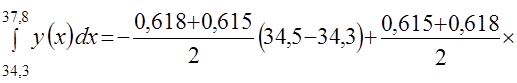
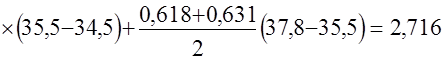 .
.
Полученные коэффициенты подставляются в систему уравнений (4.26):
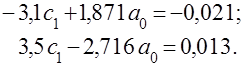
Решая эту систему, определяются
![]() .
.
Затем находится значение первой производной в начальной точке путем подстановки в уравнение (4.23) вычисленных коэффициентов и ![]() .
.
Тогда
![]() .
.
Для ![]() базисное уравнение имеет вид
базисное уравнение имеет вид
![]() или
или ![]() .
.
Таким образом, получены все параметры. Подставив в уравнение функции с гибкой структурой значение первой производной и значение ![]() , можно получить
, можно получить
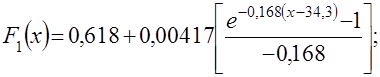
![]() .
.
Подстановкой вместо ![]() его перспективного значения на определенный год определяется ожидаемая величина коэффициента выпуска. Необходимо отметить, что основной задачей при использовании ФГС для прогноза является определение корней базисного уравнения
его перспективного значения на определенный год определяется ожидаемая величина коэффициента выпуска. Необходимо отметить, что основной задачей при использовании ФГС для прогноза является определение корней базисного уравнения ![]() , значения которых зависят от коэффициентов
, значения которых зависят от коэффициентов ![]() . Последние должны определяться из принципа оптимальной аппроксимации, заключающегося в минимизации остатка
. Последние должны определяться из принципа оптимальной аппроксимации, заключающегося в минимизации остатка ![]() и установлении таких значений коэффициентов
и установлении таких значений коэффициентов ![]() , для которых значение остатка в каждой точке таблицы исходных данных не превышает некоторой заданной величины (ошибки аппроксимации). При машинной реализации метода, базирующегося на применении ФГС, необходимо принимать допущение о дифференцируемости функции
, для которых значение остатка в каждой точке таблицы исходных данных не превышает некоторой заданной величины (ошибки аппроксимации). При машинной реализации метода, базирующегося на применении ФГС, необходимо принимать допущение о дифференцируемости функции ![]()
![]() раз, с учетом которого можно записать, что
раз, с учетом которого можно записать, что
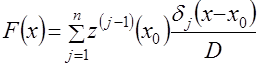 ; (4.27)
; (4.27)
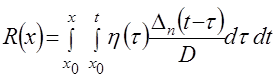 , (4.28)
, (4.28)
где ![]() – значение производной функции
– значение производной функции ![]()
![]() порядка в точке
порядка в точке ![]() ;
;
![]() – выражение, получаемое из определителя
– выражение, получаемое из определителя
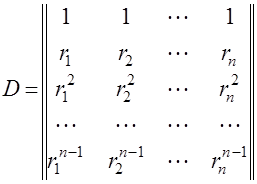 (4.29)
(4.29)
заменой последней строки определителя на функции вида ![]() ,
, ![]() ;
;
![]() . (4.30)
. (4.30)
Значения коэффициентов ![]() определяются в результате решения уравнения (4.30) путем приравнивания его к нулю. В связи с тем, что производные
определяются в результате решения уравнения (4.30) путем приравнивания его к нулю. В связи с тем, что производные ![]() неизвестны, переходят к системе линейных алгебраических уравнений [1], [2] вида
неизвестны, переходят к системе линейных алгебраических уравнений [1], [2] вида
Актуально о образовании:
Особенности развития школы слабослышащих детей
Педагогика – наука о воспитании. Одна из ее современных ветвей получила название коррекционной педагогики (от лат. сcorrection – исправляю). Это отрасль педагогической науки, которая изучает закономерности, причины возникновения отклоняющегося поведения у детей, разрабатывает пути и способы его исп ...
Эффективность уроков, проведенных по модульной
технологии
Педагогические исследования шести разработанным модульных уроков по темам: "Коррозия металлов", "Соединения металлов. Оксиды и гидроксиды металлов", "Соли металлов", "Качественное обнаружение металлов", "Нахождение металлов в природе", "Практич ...
Способы активизации мыслительной деятельности
Разнообразные задания: Задания на различение сходного материала. Это задания, требующие противопоставления сходного или в которых чередуются задачи со сходными, но неодинаковыми условиями. (Например в грамматике при изучении легко смешиваемых орфограмм: безударных А и О, приставок ПРИ - и ПРЕ-). За ...

