Модифицированный имитационным моделированием метод экспоненциального сглаживания

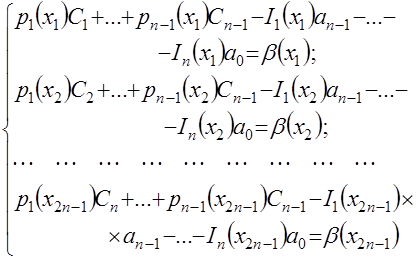, (4.31)

где , ;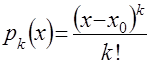

– постоянная интегрирования; ;

, , ;

; .

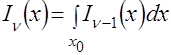Результатом решения этой системы является определение коэффициентов , что позволяет по базисному уравнению вычислить параметры . Неизвестные как следует из (4.18), (4.27), равны значениям производных функций в точке , то есть

.

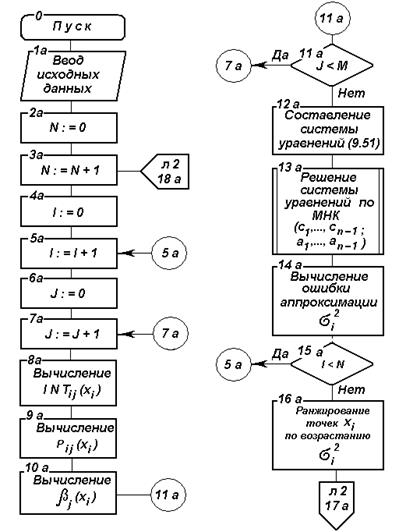
Рис. 4.6 Блок-схема алгоритма параметрического прогнозирования на основе ФГС

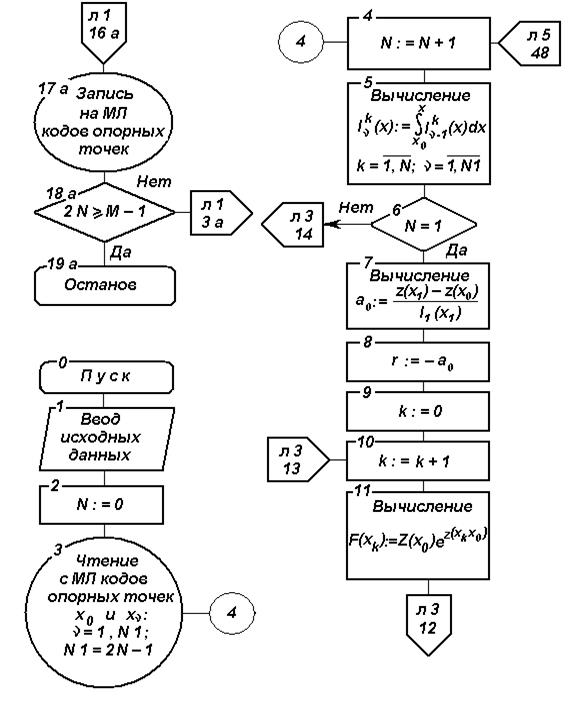
Рис. 4.6. Блок-схема алгоритма параметрического прогнозирования на основе ФГС (продолжение)

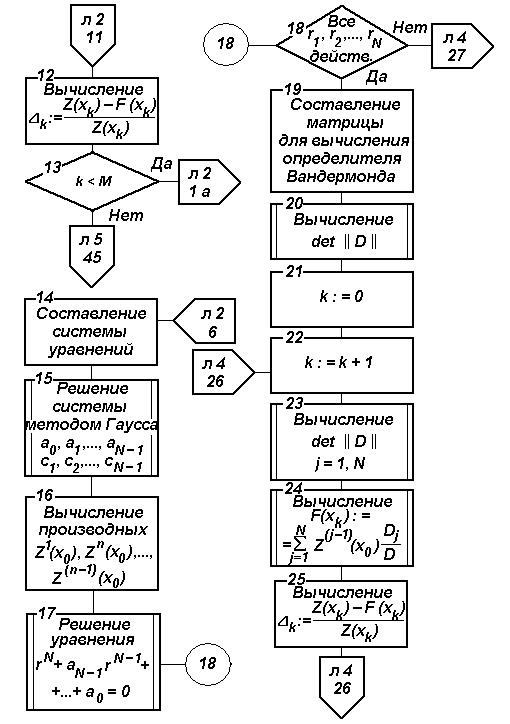
Рис. 4.6. Блок-схема алгоритма параметрического прогнозирования на основе ФГС (продолжение)

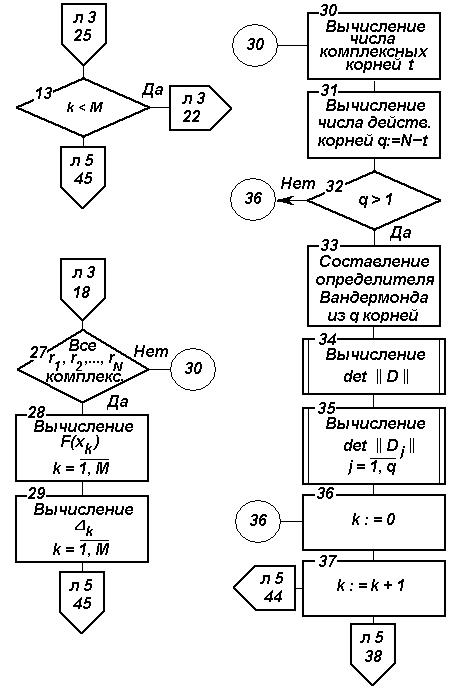
Рис. 4.6. Блок-схема алгоритма параметрического прогнозирования на основе ФГС (продолжение)

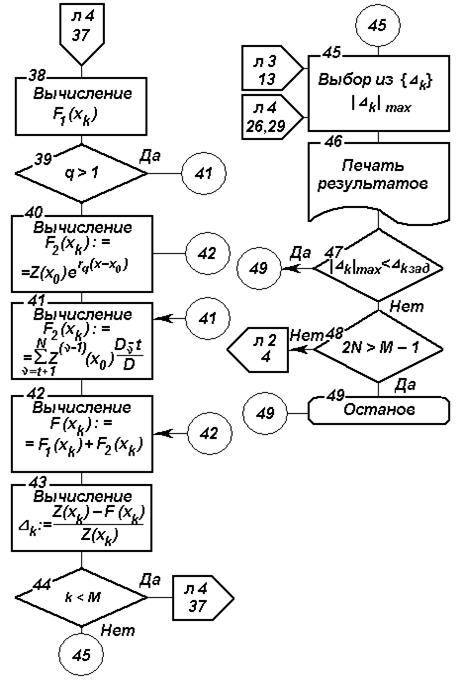
Рис. 4.6. Блок-схема алгоритма параметрического прогнозирования на основе ФГС (продолжение)

На основе изложенного разработан алгоритм параметрического прогнозирования, блок-схема которого изображена на рис. 4.6.

Согласно работам можно утверждать, что ошибка аппроксимации в значительной степени зависит от системы опорных точек и , которые необходимо выбрать для вычисления коэффициентов при неизвестных и и свободных членов системы уравнений (31). Поэтому в рамках алгоритма имеется специальная процедура выбора системы опорных точек (блоки 1–19), использование которой обеспечивает минимальную ошибку аппроксимации. Смысл этой процедуры сводится к следующему:

в качестве начальной точки последовательно выбирается каждая точка таблицы исходных данных (блоки 4а, 5а, 15а);

при зафиксированном значении вычисляются значения (блоки 6а–11а);

составляется система уравнений (4.31) (блок 12а);

решается система уравнений (4.31) по МНК и определяются значения Си , (блок 13а);

устанавливается структура модели, например в виде регрессионного уравнения

Актуально о образовании:

Формирование у учащихся умения самостоятельно пополнять знания
В настоящее время большую актуальность приобретает развитие у учащихся на уроках химии умения самостоятельно пополнять свои знания. Решение этой педагогической проблемы требует от учителя повышения всего научно-методического уровня обучения, оптимального использования внутри- и межпредметных связей ...

Наблюдения за млекопитающими
Большей частью они бывают случайными. Гораздо чаще отмечаются следы деятельности млекопитающих. Установить время начала того или иного сезонного явления в жизни животных можно лишь при условии частого посещения участка, где они в этот период находятся. Начало гона отмечают, когда на снегу появляютс ...

Сущность, задачи, система эстетического воспитания
Эстетическое воспитание — целенаправленный процесс формирования творчески активной личности, способной воспринимать, чувствовать, оценивать прекрасное, трагическое, комическое, безобразное в жизни и искусстве, жить и творить, «по законам красоты». Эстетическое воспитание включает в себя эстетическо ...