Модифицированный имитационным моделированием метод экспоненциального сглаживания

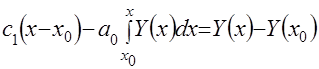. (4.25)

Из этого уравнения видно, что оно содержит неизвестные величины. Теперь значение интеграла можно вычислить, так как функция УМ задана таблицей, а для определения и можно образовать систему двух уравнений с двумя неизвестными на основе уравнения (4.25). Это нетрудно сделать, если подставить в (4.25) значение еще двух точек, взятых из временного ряда. Тогда

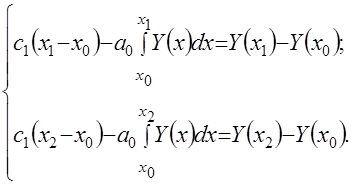(4.26)

После вычисления данных интегралов находятся неизвестные коэффициенты и . Затем определяется значение первой производной путем подстановки в уравнение (4.23) , и . Корень базисного уравнения равен параметру со знаком минус. Вычисленные параметры подставляются в формулу ФГС (4.19) для получения математического выражения формы связи между и .

В качестве примера применения функции с гибкой структурой для прогнозирования в военном деле рассматривается задача по определению вида зависимости между коэффициентом выпуска серийных образцов условных технических систем и объемом задач, выполняемых с помощью данных образцов. Эта зависимость в дальнейшем используется для получения прогноза. Исходные данные представлены в табл. 1.

Таблица 1

Из этой таблицы выбираются значения трех опорных точек, одна из которых (начальное значение) должна лежать в середине ряда с тем, чтобы полученная функция одинаково точно приближала данное значение как в конце, так и в начале ряда. Следовательно,

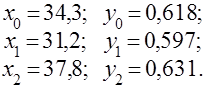
Определяются коэффициенты уравнения (4.26):

Следующий шаг – переход к вычислению необходимых интегралов (рис. 4.5).

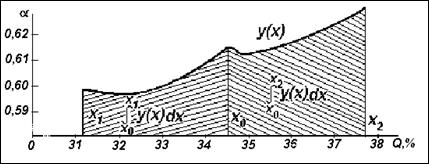
Рис. 4.5 Определение необходимых интегралов для ФГС

Интеграл вида 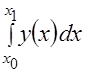есть площадь, ограниченная графиком и значениями , равными 34,3 и 31,2. Так как верхний предел интеграла меньше нижнего, то значение интеграла отрицательное. Площадь, ограниченная значениями равными 34,3 и 31,2, будет складываться из площадей трех трапеций:

Актуально о образовании:

Возрастные психофизиологические особенности детей младшего школьного возраста
Для организации и разработки содержания проектной деятельности детей 2-4 классов, необходимо изучить возрастные психофизиологические особенности детей данного возраста. В младшем школьном возрасте большие изменения происходят в познавательной сфере ребенка. Память приобретает ярко выраженный познав ...

Описание УМК
В учебном процессе основной формой обучения было и остается классно-урочная система. С появлением компьютеров и компьютерных информационных технологий эту систему можно сделать более эффективной, интересной и практичной. Создав УМК по теме «Основы логики» для студентов I курса, облегчается труд учи ...

Решение задач на совместное движение
Начиная с 5-го класса, ученики часто встречаются с этими задачами. Еще в начальной школе учащимся дается понятие «общей скорости». В результате у них формируются не совсем правильные представления о скорости сближения и скорости удаления (данной терминологии в начальной школе нет). Чаще всего, реша ...