Модифицированный имитационным моделированием метод экспоненциального сглаживания

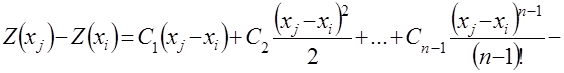
(4.32)

параметры которого определены выше, и задают ошибку аппроксимации по зависимости (блок 14а)

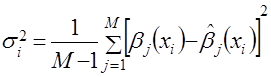, (4.33)

где – число наблюдений над прогнозируемой характеристикой;

осуществляются ранжировка исходных данных по возрастанию , выбор опорных точек по правилу (блок 16а)

и их запись;

описанная процедура повторяется для каждого значения (блоки 2а, За, 18а).

После выбора опорных точек в алгоритме предусмотрены операторы по подготовке к составлению системы уравнений порядка. С этой целью по соответствующим зависимостям методом численного интегрирования (методом трапеций) вычисляются , а также значения и (блок 5). При этом

.

Если число членов ФГС-модели , то значения параметров функции и относительного отклонения функции от в -й точке рассчитываются в соответствии с выражениями блоков 7–3. На основе выбора из множества значения и сравнения его с заданным (блоки 45, 47), принимается решение либо продолжать усложнять модель, либо удовлетвориться достигнутой сложностью. При осуществляется составление системы уравнений порядка вида (4.31) (блок 14) и решение ее методом Гаусса относительно параметров и постоянных интегрирования (блок 15).

В блоке 16 осуществляется вычисление параметров

по зависимостям

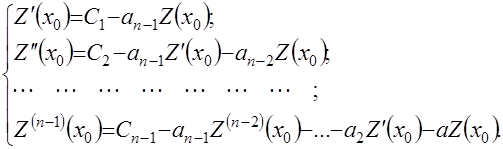(4.34)

Вычисление корней базисного уравнения производится методом Ньютона с использованием стандартной программы (блок 17). Поскольку в общем случае корни уравнения могут быть действительными, комплексными или действительными и комплексными, в блоках 18, 27 производится их анализ с целью определения дальнейшей расчетной схемы. При условии, что все корни действительные, функция принимает вид

Актуально о образовании:

Коррекционно-развивающая программа работы с детьми младшего школьного возраста, склонными к проявлению агрессивности
Разрабатывая коррекционно-развивающую программу для детей склонных к агрессивному поведению, мы обратили внимание на важность взаимодействия социального педагога с классным руководителем, преподавателями, работающими с данной категорией детей, а так же с родителями. Проводя работу в этом направлени ...

Творчество в деятельности учителя технологии и его влияние на качество обучения учащихся
Ежедневно школьный звонок призывает в классы миллионы учителей. Вот они энергично идут по школьным коридорам, открывается дверь в класс, и начинается великое таинство, имя которому - педагогическое творчество. Творческая педагогика, творческий учитель - как они необходимы сейчас. Можно построить за ...

Уровневая дифференциация обучения на основе обязательных результатов
В данной технологии предлагается введение двух стандартов: для обучения (уровень, который должна обеспечить школа интересующемуся, способному и трудолюбивому выпускнику) и стандарта обязательной общеобразовательной подготовки (уровень, которого должен достичь каждый). Пространство между уровнями об ...