Модифицированный имитационным моделированием метод экспоненциального сглаживания

.

Аналогичная процедура повторяется до тех пор, пока величина критерия фильтрации уменьшается или увеличивается в зависимости от его содержания (при этом исходная информация делится на две выборки: обучающую и проверочную). Для практических расчетов в качестве такого критерия рекомендуется принимать среднеквадратическую ошибку аппроксимации модели на проверочной выборке, которая, как установлено в работе, при увеличении числа уровней фильтрации, а, следовательно, сложности модели, достигает экстремального значения. Сложность модели (измеряется числом ее членов), соответствующая экстремальному значению критерия, является оптимальной. На последнем уровне фильтрации фиксируется «частное описание», значение которого минимально. На предпоследнем уровне выбираются «частные описания», являющиеся аргументами последнего уровня, и т.д. Так как «частные описания» являются функцией двух аргументов, их коэффициенты легко определяются по небольшому количеству исходных данных. Исключая промежуточные переменные можно получить модель исследуемых характеристик объекта прогнозирования в виде аналога «полного описания»

,

где в общем случае .

Как известно, особые трудности при увеличении числа членов в разложении Тейлора связаны с получением аналитических зависимостей для определения вектора коэффициентов . Из работы следует, что

,

где – вектор-столбец размером сглаженных значений процесса

;

– вектор-столбец размером неизвестных коэффициентов

;

– матрица размером , элементы которой, соответствующие -й строке и -му столбцу, вычисляются по зависимости

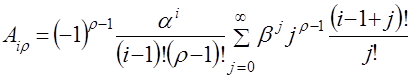. (4.13)

В связи с тем, что сглаженные значения процесса могут быть определены по зависимости

вектор выражается зависимостью . (4.14)

Анализ зависимости (4.13) показывает, что наибольшую сложность вызывает вычисление суммы бесконечного ряда, представляющего собой произведение степеней показательной функции и отношения факториалов, которое можно упростить путем несложных преобразований:

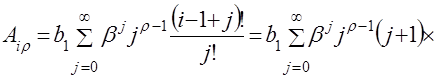
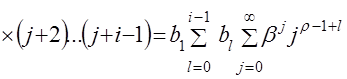, (4.15)

где ;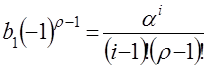

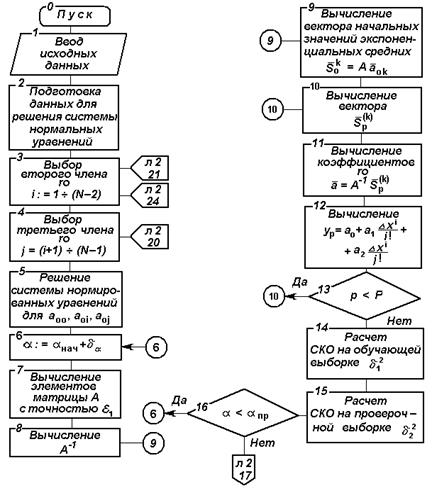
Рис. 4.4 Блок-схема алгоритма прогнозирования по методу модифицированного экспоненциального сглаживания

Актуально о образовании:

Формирование предметной отнесенности слова
Анализируя развитие значения слова в онтогенезе, Л. С. Выготский писал: «Речь и значение слов развивались естественным путем, и история того, как психологически развивалось значение слова, помогает осветить до известной степени, как происходит развитие знаков, как у ребенка естественным образом воз ...

Технология обработки разных материалов на занятиях по художественному труду
Вязание как отрасль декоративно-прикладного искусства. Вязание на спицах – одна из областей традиционного народного искусства, которая исторически приобрела промысловое значение и развивается в наши дни. Это несложный и очень увлекательный вид рукоделия. До нас дошли экземпляры вещей, связанных в I ...

Наблюдения за грибами
Плодоношение съедобных грибов наблюдается в определенной последовательности. Одни виды появляются весной, другие - летом, третьи - только в конце лета - начале осени. Для образования плодовых тел разных видов грибов необходимы оптимальная температура и влажность лесной подстилки и верхних слоев поч ...