Модифицированный имитационным моделированием метод экспоненциального сглаживания

Для прогнозирования характеристик образцов техники, математическое описание которых имеет вид

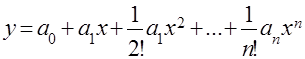, (4.10)

целесообразно применять метод экспоненциального сглаживания. Сложившаяся практика использования этого метода предполагает ограничение числа членов ряда Тейлора

,(4.11)

аппроксимирующего выражение (4.10), несколькими членами .

В зависимости (4.11) – -я производная функции по переменной в точке ; ; – число наблюдений; – значение величины шага упреждения.

Для условий, когда ошибки прогнозирования не удовлетворяют заданным требованиям, можно осуществить анализ их источников. Известно [4], что точность прогнозной задачи можно определить по зависимости

, (4.12)

где ;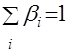

– погрешность, обусловленная приближенностью исходной информации;

– погрешность, связанная с методом прогнозирования;

– погрешность, вызванная неточностью вычислений;

– нерегулярная погрешность, обусловленная вероятностью непредсказуемых в настоящее время событий, влияющих на характер изменения прогнозируемой величины.

Одной из наиболее весомых является методическая ошибка, зависящая от числа членов разложения. В работах приводятся аналитические зависимости для выполнения параметров аппроксимирующего многочлена при . Вывод таких зависимостей для представляет значительные трудности. Кроме того, любое увеличение числа членов выражения (4.11) влечет за собой потребность увеличения объема исходных данных, необходимых для определения оценок начальных значений коэффициентов (методом наименьших квадратов или в более общем случае методом максимального правдоподобия), далее предлагается модификация метода экспоненциального сглаживания, основанная на принципах группового учета аргументов. Сущность метода заключается в том, что математическая модель объекта прогнозирования

,

называемая в соответствии с терминологией работы [1] его «полным описанием», заменяется набором «частных описаний» вида

.

По принятому критерию, значение которого вычисляется для каждого «частного описания», из множества отбирается некоторое число, называемое «свободой выбора», наиболее регулярных описаний, образующих подмножество . Вычисленные значения промежуточных аргументов принимаются в качестве аргументов «частных описаний» следующего уровня фильтрации, то есть

Актуально о образовании:

Общая характеристика содержания и средств обучения в системе М. Монтессори
В видении монтессори-педагога каждый ребенок от рождения наделен ему одному свойственным потенциалом развития. Раскрыться этот потенциал может только в собственной деятельности ребенка. Путь развития и совершенствования у каждого человека свой. Задача образования при этом сводится к тому, чтобы соз ...

Причины неуспеваемости учащихся по химии в средней школе
Психологические исследования последних лет позволяют учителю-предметнику получить весьма важные сведения о типичных возрастных особенностях сформированности у учащихся определенного возраста различных интеллектуальных умений и других качеств личности. Эти сведения, к сожалению, не стали исходной ос ...

Ознакомление детей 7 лет с немецкой культурой
1. развитие коммуникативных навыков у детей, творческой активности и самостоятельности. 2. расширение представлений о культуре, традициях, праздниках в Германии. 3. развитие творческих, художественных, актёрских способностей. 4. вызвать у детей желание участвовать в коллективной деятельности. Работ ...