Что понимается под названием вычислительный эксперимент
Вероятность 
называют доверительной вероятностью, а границы интервала 
, в которых с заданной доверительной вероятностью заключена ошибка метода – доверительными границами.
Из теории вероятностей известно, что при нормальном законе распределения вероятность отклонения случайной величины 
от ее математического ожидания 
менее, чем на 
равна
, (4)
где 
– функция Лапласа (интеграл вероятностей);
– аргумент функции Лапласа;
– среднее квадратическое отклонение величины .
Также известно, что если производится большое число 
опытов, то среднее арифметическое 
есть также случайная величина, приближенно распределенная по нормальному закону с математическим ожиданием 
и средним квадратическим отклонением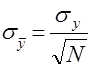 
.
Из сказанного следует, что вероятность любого отклонения 
может быть вычислена по формуле
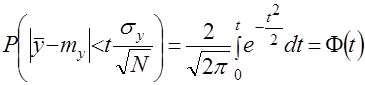. (5)
Положим
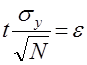, (6)
тогда получим
. (7)
Сравнивая выражения (3) и (7), найдем условие, при котором ошибка метода не превысит величину 
с вероятностью :
. (8)
Задаваясь доверительной вероятностью , найдем из уравнения (8) с помощью таблиц функции Лапласа численное значение 
. Подставив далее величину в выражение (6), получим формулу для вычисления искомого числа испытаний , при котором выполняется условие (8):
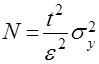. (9)
Из формулы (9) видно, что для определения необходимо еще знать величину дисперсии 
. Так как она неизвестна, обычно поступают следующим образом. Задаются некоторым достаточно большим значением 
и находят приближенное значение (статистическую оценку) дисперсии по формуле
Актуально о образовании:
Модульная технология
Модульное обучение зародилось в конце второй мировой войны в ответ на обострившиеся социально-экономические нужды, когда были крайне необходимы системы обучения профессиональным умениям в относительно короткий период. Были детально изучены индустриальные задачи и разработаны инструкции по их теорет ...
Выявление меры связи между характеристиками мышления и
успешностью в обучении математике
После проведения исследований характеристик мышления и получения результатов проверим гипотезу о связи между мышлением учеников и их достижениями в математике. Попробуем установить, влияет ли уровень развития мышления учащихся на их успешность в обучении математике, зависят ли результаты обучения о ...
Характеристика содержания образовательной области «Художественное
творчество» в программе «Детство»
Основной целью дошкольного образования является целостное развитие личности. Выделяются следующие компоненты цели: развивающие, воспитательные, образовательные и практические. Развивающий компонент цели предусматривает развитие психических процессов – эстетическое сознания, памяти, творческого вооб ...