Что понимается под названием вычислительный эксперимент

Статистическая обработка и оценка точности результатов моделирования основывается на предельных теоремах теории вероятностей: теореме Чебышева и теореме Бернулли.

Согласно теореме Чебышева, при неограниченном увеличении числа независимых испытаний среднее арифметическое значение случайной величины сходится по вероятности к математическому ожиданию этой величины, то есть

, (1)

где – сколь угодно малое положительное число,

.

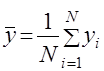Теорема Бернулли доказывает, что при неограниченном увеличении числа независимых испытаний частота наступления случайного события сходится к вероятности этого события, то есть

. (2)

Пусть случайная величина характеризуется математическим ожиданием и дисперсией . В качестве приближенного значения величины берется среднее арифметическое значение , определяемое по результатам независимых испытаний. Отклонение величины от искомого математического ожидания и есть ошибка метода. Величина , удовлетворяющая неравенству , называется точностью оценки.

Из теоремы Чебышева следует, что ошибка метода может быть оценена лишь вероятностно, с определенной степенью достоверности. Обозначим через вероятность того, что выполняется неравенство :

. (3)

Вероятность характеризует степень достоверности оценки, ее надежность. Это означает, что с надежностью можно быть уверенным, что среднее арифметическое значение не выйдет за пределы интервала , то есть, что

.

Актуально о образовании:

Новый подход к содержанию образования
Каким будет наше российское образование завтра? На каких принципах должно строится образование сегодня? Вот вопросы, на которые хотел бы получить ответ любой здравомыслящий человек нашего общества. Ответы на эти вопросы можно найти в статьях наших ученых, которые рассматривают новые подходы к содер ...

Объект и программа исследований
Объект 1: 10 классы средней школы №1 г.п. Корма. Эти классы были выбраны нами не случайно, т.к. они не специализированы по химии, разные по успеваемости. Работа в 10-х классах строится по программе средней школы 1999 г., и в соответствии с этой программой учащиеся в 10-х классах изучают неорганичес ...

Синонимы в лексико-семантической системе языка
Синонимы от греческого synonymos – одноименный) – это слова, различные по звучанию, но тождественные или близкие по значению, нередко отличающиеся стилистической окраской: храбрый – смелый, отважный, бесстрашный, безбоязненный, неустрашимый, удалой, лихой. Группа слов, состоящая из нескольких синон ...