Полные факторные планы испытаний

Приведенные в табл. 1 и 2 матрицы планирования обладают свойствами ортогональности, симметричности и нормировки.

Свойство симметричности относительно центра опыта заключается в том, что алгебраическая сумма элементов вектор-столбцов каждого из факторов равна нулю:

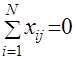; ; . (4)

Условие нормировки подтверждается равенством суммы квадратов элементов каждого столбца числу опытов:

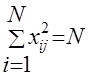; . (5)

Свойство ортогональности определяется равенством нулю произведений любых двух вектор-столбцов:

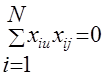;. (6)

Предполагается, что при перемножении элементов с одноименными знаками получаем , с разноименными .

Свойство ортогональности позволяет резко уменьшить трудоемкость вычислений коэффициентов регрессии, так как матрица нормальных уравнений становится диагональной, причем ее диагональные элементы равны числу испытаний , заданных матрицей ПФП.

Воспользуемся матрицей планирования (табл.1) для получения уравнения регрессии вида

. (7)

При вычислении оценок коэффициентов регрессии по формуле последовательно получим

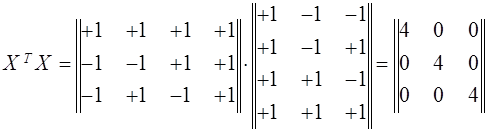
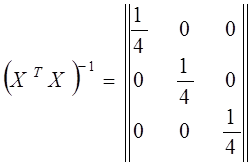
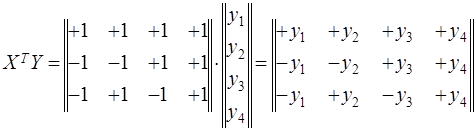
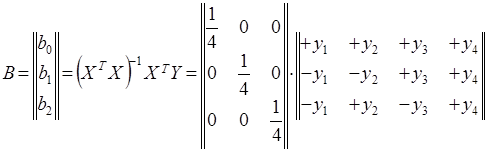
Отсюда

; ;

; .

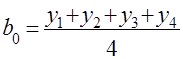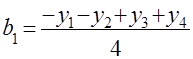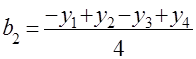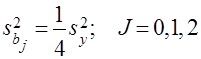Таким образом, каждый из коэффициентов вычисляется независимо и по простой формуле, которая в общем случае имеет вид

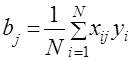. (8)

Поскольку все диагональные элементы матрицы ошибок равны между собой, каждая из оценок получена с одинаковой (и минимальной) дисперсией

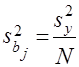, (9)

где – ошибка опыта.

Рассмотренные ПФП являются оптимальными в том смысле, что при их реализации для данного числа испытаний определитель матрицы ошибок минимален. Геометрически это означает, что сведен к минимуму объем эллипсоида рассеивания оценок параметров. Важным свойством полученных планов является также рототабельность, которая заключается в том, что точность предсказания значений выходной характеристики одинакова на равных расстояниях от центра плана и не зависит от направления.

Актуально о образовании:

Внеклассные мероприятия по химии как фактор развития самостоятельности
Одним из главных требований в преподавании химии являются твердые знания по основному предмету. Каждый учитель должен уметь ориентироваться в приоритетных направлениях своей деятельности, анализировать информацию и принимать правильные решения. Он должен заложить твердые разносторонние знания, фунд ...

Специфика педагогического творчества
Специфика педагогического творчества заключается в том, что его должно рассматривать как сотворчество учителя и ученика, несмотря на то, что они субъекты разных видов деятельности. В.И. Загвязинский так пишет об этом: "Учитель занят педагогическим творчеством, ученик - предметным (изобразитель ...

Учебные лекции по астрономии, читаемые в планетарии
Учащиеся не всегда могут самостоятельно ознакомиться с различными небесными явлениями. Этому препятствует много причин: неблагоприятная погода, несовпадение времени явлений с днями наблюдений, неосуществимость наблюдений редких и медленно протекающих явлений, а также явлений, принципиально недоступ ...