Анализ программ математических кружков

В условии задачи мы имеем: полученное число должно делиться на 15. Что это значит? Что мы должны рассмотреть признак делимости числа 15. То есть b либо равно 5, либо 0.

По признаку делимости на 5: b=0 или b=5. Рассмотрим оба случая.

а). Пусть b=0.

Полученное число a150 должно делиться на 15. (Подобно первой задаче находим число а). О признаке делимости на 5 мы сказали ранее, а на 3 число делится - тогда и только тогда, когда сумма его цифр, равная a+1+5, делится на 3. Отсюда получаем, что а=3, 6, 9.

б). Рассмотрим второй случай. Пусть b=5.

Здесь получаем, что полученное число a10b делится на 5, а на 3 - тогда и только тогда, когда сумма его цифр, равная а+1+5+5, делится на 3. Получаем, что а=1, 4, 7.

Ответ: четырехзначные числа равны: 3150, 6150, 9150, 1155, 4155, 7155.

3). Найдите наибольшее натуральное число, делящееся на 36, в записи которого участвуют все 10 цифр по одному разу.

Решение: Число делится на 36 тогда и только тогда, когда оно делится на 9 и на 4. Проверим, что сумма всех десяти цифр делится на 9 (1+2+3+4+5+6+7+8+9=45; 45: 9=5). Поэтому любое число, в записи которого участвуют все 10 цифр по одному разу, делится на 9. Самым большим таким числом является число 9876543210. Но оно не делится на 4 (ибо число делится на 4 тогда и только тогда, когда две его последние цифры образуют число, делящееся на 4). Нужно добиться делимости на 4, минимально уменьшив при этом число. Очевидно, число 9876543120 делится на 4. Больше него только числа 9876543210 и 9876543201, которые на 4 не делятся.

Ответ: 9876543120.

Целесообразно дать учащимся подобные задачи для самостоятельного решения.

4). Замените звёздочки в записи числа 72*3* цифрами так, чтобы число делилось без остатка на 45.

5). Найти натуральные числа, дающие при делении на 2, 4, 5, 6 остаток 1, и, кроме того, делящиеся на

6). Заполните столбики таблицы, предлагаемыми числами:

155, 192, 304, 766, 845, 900, 975, 5555, 6000.

7). Докажите, что число записанное шестью одинаковыми цифрами, делится на 3, 7, 11, 13, 37.

В заключении хотелось бы представить участникам кружка четыре изумительных десятизначных числа:

2 438 195 760

3 785 942 160

4 753 869 120

4 876 391 520

В каждом из них есть все цифры от 0 до 9, причем каждая цифра только по одному разу и каждое из этих чисел делится на 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, и 18. (Можно в виде домашнего задания предложить учащимся проверить несколько чисел).

Вступительное слово учителя.

"В дни моей юности я в свободное время развлекался тем, что составлял… магические квадраты" - Бенджамин Франклин.

Одно из самых загадочных произведений изобразительного искусства хранится в Кунстхалле города Карлсруэ. Речь идет о гравюре Альбрехта Дюрера "Меланхолия I".

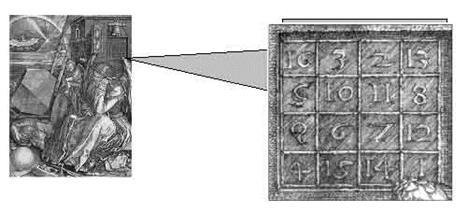
Значимая деталь, изображенная на гравюре "Меланхолия I" - составленный впервые в европейском искусстве магический квадрат 4 Х 4. Сумма чисел в любой строке или столбце равна 34. Два средних числа в нижнем ряду указывают дату создания картины 1514 год.

Актуально о образовании:

Формы и методы формирования исследовательской компетенции старшеклассников в процессе обучения английскому языку
В данном параграфе будут рассмотрены формы и методы, способствующие формированию исследовательской компетенции старшеклассников на уроках английского языка. Для начала мы опишем основные формы, применяемые нами в процессе формирования исследовательской компетенции учащихся. Обычно выделяют формы ор ...

Творческие находки учителей технологии в создании увлекательных уроков: анализ практической деятельности
Три основных вопроса каждодневно встают перед учителем при подготовке к занятиям: Для чего учить? Чему учить? Как учить? Программы, учебники, методические пособия существенно помогают ему при решении первых двух вопросов. Правда и тут он многое должен додумать сам, учитывая конкретные задачи обучен ...

Констатирующий этап эксперимента: описание диагностических методик по определению уровня творческих способностей младших школьников
Следующим этапом нашей работы был сбор сведений об уровне развития творческих способностей младших школьников. Мы сделали это, опираясь на данные, полученные в ходе работы с ученическим коллективом 1 класса средней школы №44 г. Краснодара. Детям предлагался ряд заданий, которые будут описаны ниже, ...