Анализ программ математических кружков

3). В нашей стране проживают около 250 млн. человек. Если все люди встанут в одну шеренгу, то какой длины будет эта шеренга? (Пусть каждый человек занимает место длиной в 50см).

4). Каких размеров достигает обыкновенный комар, увеличенный в миллион раз? Длина комара приблизительно равна 5мм.

5). Узнайте свой рост, увеличенный в миллион раз?

6). Сколько километров займет миллион людей, построенных в один ряд плечом к плечу?

3). Рассказ учителя о числах - карликах.

В конце занятия обобщим знания, полученные на данном занятии.

Сверхгигант и сверхлилипут.

Наши беседы о великанах и карликах из мира чисел были бы неполны, если не рассказать одной изумительной диковинке этого рода - диковинке, правда, не новой, но стоящей дюжины новинок. Чтобы подойти к ней, начнем со следующей, на вид весьма незамысловатой задачи.

Какое самое большое число можно написать тремя цифрами, не употребляя никаких знаков действий?

Решение:

Хочется ответить: 999,-но, вероятно, вы уже подозреваете, что ответ иной; иначе задача была бы чересчур проста. И, действительно, правильный ответ пишется так:

Выражение это означает: "девять в степени девять в девятой степени".

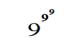
Если хватит терпения выполнить перемножение девяти девяток, вы получите число: 387 420 489. Другими словами: нужно составить произведение из стольких девяток, сколько единиц в результате умножения: 9 · 9 · 9 · 9 · 9 · 9 · 9 · 9 · 9. Достаточно только начать вычисление, чтобы ощутить огромность ожидаемого результата: 9387420489, т.е. произведение 387 420 489 девяток. Придется сделать круглым счетом 400 миллионов умножений.

Познакомившись с этим замаскированным гигантом, попытайтесь найти его противоположность. (Соответствующий числовой лилипут получится, если разделим единицу на это число. Будем иметь: 1/9387420489).

Архимед вычислил некогда, сколько песчинок заключал бы в себе мир, если бы весь он, до неподвижных звезд, наполнен был тончайшим песком. У него получился результат, не превышающий единицы с 63 нолями. Наше число состоит не из 64, а из 370 миллионов цифр - следовательно, оно неизмеримо превышает огромное число Архимеда.

В качестве домашнего задания можно предложить посчитать, сколько песчинок понадобится, чтобы устлать весь пол в квартире каждого учащегося в один ряд. Для этого необходимо узнать у родителей метраж квартиры. Размер песчинки приблизительно равен 0,125миллиметра.

Учащиеся 6 класса уже владеют понятиями: "простые и составные числа", "Делители натурального числа", НОК и НОД, умеют применять свойства и признаки делимости. Поэтому в объяснении нового для 5-классников материала будут принимать участие ученики 6 класса, заранее подготовленные с учителем.

Рассмотри задачу: в доме, где всего один подъезд - 35 квартир. Может ли дом быть семиэтажным? (Сколько тогда квартир на одном этаже). А четырехэтажным? Сколько этажей еще может быть в доме? Таким образом, мы можем сказать, что количество этажей - это число, на которое 35 делится без остатка, то есть нацело. Если одно натуральное число нацело делится на другое натуральное число, то первое называют кратным второму, а второе - делителем первого. Например, 35: 7 = 5, из этого следует, что 35 кратно 7, а 7 - делитель числа 35.

Можем ответить на вопросы нашей задачи: если на каждом этаже по одной квартире (что маловероятно), то этажей 35. Следуя данному рассуждению, мы делим 35 на 5 и получаем 7. То есть дом может быть пятиэтажным, на каждом этаже по 7 квартир. А четырехэтажным дом не может быть, поскольку 35 не делится на 4 нацело.

Актуально о образовании:

Исследование межличностных отношений младших школьников
Задачами нашего исследования являются: 4. Осуществление теоретического понятия «межличностные отношения». 5. Изучение межличностных отношений как фактора личностного развития младшего школьника. 6. Выявление социометрического статуса младших школьников. Диагностировать структуру межличностных взаим ...

Методика формирования пространственного мышления учащихся основной школы при изучении элементов геометрии
Известно, что геометрия как наука, первоосновы которой излагаются в школе, имеет своим предметом изучение пространственных форм и отношений реального мира. Научное познание этих форм и отношений возможно при наличии у человека развитого мышления и воображения. Такие качества приобретаются жизненным ...

Исследование составляющей когнитивного развития учеников – мышления и его связей с учебными достижениями по математике
С целью установления связей между характеристиками мышления и учебными достижениями по математике было проведено исследование в ОМК. Исследование проводилось в октябре – ноябре 2011 года, в котором были задействованы учащиеся 7-го класса (всего 13 человек). Исследование проводилось в двух направлен ...