Методика формирования пространственного образа на уроках геометрии

К таким заданиям можно отнести следующие виды задач.

а) Задачи на изображение пространственной фигуры, заданной словесным описанием.

Пример 1. В пирамиде с основанием в виде правильного треугольника одно из боковых ребер перпендикулярно плоскости основания. Что представляют собой грани такой пирамиды? Каким образом проходит высота пирамиды? Изобразите данную пирамиду?

Пример 2. В основании наклонной призмы правильный пятиугольник. Сколько граней у данной призмы? Какими геометрическими фигурами являются ее грани? Могут ли среди боковых граней быть прямоугольники? Изобразите данную призму .

б) Задачи, в которых требуется достроить фигуру или восстановить чертеж.

Пример. 1. Достройте изображение фигуры до куба:

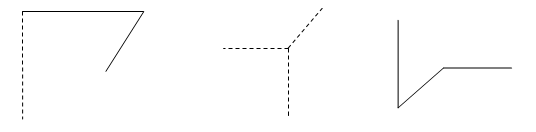
Пример 2. Достройте изображение фигуры до треугольной пирамиды:

Пример 3. Достройте изображение фигуры до произвольного многогранника:

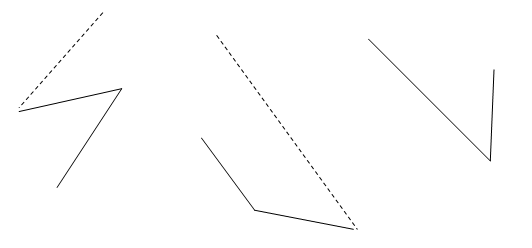
Пример 4. Достройте изображение многогранников по заданным вершинам:

а) треугольная пирамида:

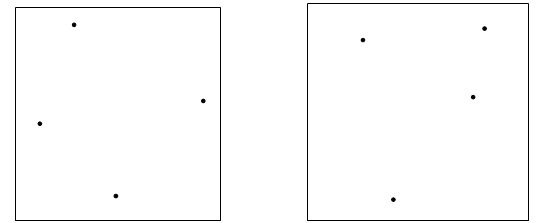
б) треугольная призма:

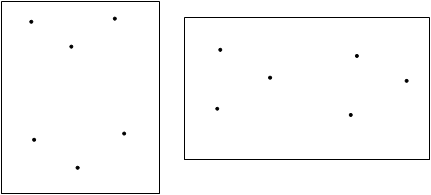
в) Задачи на построение и использование разверток пространственных фигур.

Пример 1. Нарисуйте разные развертки: а) правильного тетраэдра, б) куба.

Пример 2. Дан прямоугольный параллелепипед ABCDA1B1C1D1 (AB = BC) как провести на его поверхности кратчайшую линию, соединяющую вершины В и D1 (ответ может быть получен при помощи развертки двух смежных граней)?

Пример 3. Постройте развертку наклонной треугольной призмы.

г) Задачи, в которых по наглядному изображению или словесному описанию пространственного объекта требуется построить ее проекции.

Пример 1. Какая фигура может быть проекцией: а) отрезка, б) треугольника на данную плоскость (рассмотреть различные направления проектирования)?

Пример 2. Какое наименьшее число сторон может иметь параллельная проекция на плоскость выпуклого многогранника, имеющего n граней?

Пример 3. Многогранник имеет n вершин. Показать, что существует его параллельная проекция на плоскость, имеющая: не менее четырех вершин, не более n – 1 вершины.

д) Задачи, в которых по заданной проекции пространственного объекта необходимо восстановить его наглядное изображение.

Пример. Нарисуйте многогранник, заданный проекциями на три попарно перпендикулярные плоскости:

Развитие и совершенствование умений решать геометрические задачи обуславливает графическая культура учащихся, их умения выполнять рисунки, способность и навыки к визуализации задачи. Развитию конструктивных умений и навыков активно способствует приведенная группа задач. Кроме того, все они направлены на развитие пространственных представлений и воображения. Ведь в процессе решения таких задач, прежде чем изобразить пространственный объект с помощью рисунка или чертежа, необходимо отчетливо представить его, мысленно выполнить определенные конструктивные операции с его элементами. Задачи, выполняемые без применения чертежных инструментов, развивают глазомер, точность движений, что также является характеристикой развитых пространственных представлений.

Как уже было сказано, чертеж является важнейшим средством формирования и развития пространственных представлений. При этом необходимо обращать внимание на рассмотрение различных изображений одного и того же тела. Дело в том, что, привыкая работать с шаблонными изображениями пространственных фигур, учащиеся оказываются беспомощными, когда им надо создать образ по чертежу, на котором пространственный объект расположен нетрадиционно. Выполнение таких изображений и работа с ними способствуют совершенствованию умения рассматривать объект с различных точек зрения, удерживая его образ в памяти, анализировать созданный пространственный образ, менять пространственное положение объекта.

Развитию этих умений также способствуют задачи, в которых требуется достроить пространственную фигуру или восстановить чертеж, выполняя который необходимо сначала представить пространственный объект, потом сопоставить его с данными элементами чертежа. При этом по одним и тем же элементам (отрезкам, точкам) иногда возможны различные изображения фигуры.

Большую роль для развития умений оперировать созданным пространственным образом играют задачи на построение и использование разверток пространственных фигур. В процессе построения развертки необходимо мысленно развернуть геометрическую фигуру, сопоставить полученный результат с наглядным изображением (или существующим представлением), осуществлять анализ и синтез пространственного образа, удерживая его в памяти, изменять пространственное положение и структуру образа. В результате этих действий получен новый образ – развертка.

Актуально о образовании:

Воспитание патриотизма на уроках музыки в начальной школе
Воспитательные средства урока музыки Развитие музыкальной культуры учащихся начальных классов при­обретает новое направление. Ведущую идею тематического содержания программы можно сформулировать в двух аспектах: § во-первых, о месте музыки в жизни человека § во-вторых, о роли музыки в воспитании па ...

Основные принципы и способы повышения интереса к учебному материалу
Существует огромное количество ценностей в этой жизни. Одни мы игнорируем, другим следуем, третьи презираем, четвертые… Но среди них есть одна, безоговорочная для каждого нормального человека, - свобода! Никто из нас не любит навязанных действий, чуждый решений, отсутствия выбора. И особенно не люб ...

Нравственные отношения учителя и учеников в педагогической этике
В педагогической этике рассматриваются нравственные отношения учителя с учащимися. Субъектом нравственных отношений в педагогической среде является учитель. Будучи основным звеном в учебно-воспитательном процессе, он осуществляет самое широкое взаимодействие с учащимися, их родителями. Поэтому он я ...