Выявление связи между уровнем концентрации внимания учащихся и их учебными достижениями по математике
Найденное значение 
является приближенным, поскольку в рассмотренном примере есть так называемые связанные ранги. В этом случае лучший результат дает применение следующей формулы, которая эквивалентна предыдущей:
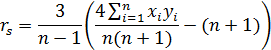
Вычислим по предыдущим данным ранговый коэффициент корреляции Спирмена по этой формуле. Имеем:
Значение свидетельствует о слабой прямой связи между уровнем концентрации внимания учащихся и их учебными достижениями по математике.
Вычислим для наших данных коэффициент корреляции Пирсона.
|
ФИ ученика |
Кол-во баллов за тест (x) |
Уровень концентрации внимания |
|
|
|
|
Елагин |
23 |
73 |
529 |
5329 |
1679 |
|
Калиманов |
18 |
74 |
324 |
5476 |
1332 |
|
Дольнев |
19 |
73 |
361 |
5329 |
1387 |
|
Киселёва |
18 |
83 |
324 |
6889 |
1494 |
|
Фёдорова |
17 |
83 |
289 |
6889 |
1411 |
|
Богданов |
19 |
54 |
361 |
2916 |
1026 |
|
Суббота |
10 |
64 |
100 |
4096 |
640 |
|
Луц |
13 |
66 |
169 |
4356 |
858 |
|
Колесников |
20 |
82 |
400 |
6724 |
1640 |
|
Мащенко |
10 |
49 |
100 |
2401 |
490 |
|
Коркос |
8 |
55 |
64 |
3025 |
440 |
|
Кладка |
16 |
69 |
256 |
4761 |
1104 |
|
Фиткулов |
14 |
58 |
196 |
3364 |
812 |
|
∑ |
205 |
883 |
3473 |
61555 |
14313 |
Актуально о образовании:
Методы воспитательной работы с младшими школьниками в условиях
дополнительного образования
педагогический школьник внеклассный образование Содержание и многообразие форм учебно-воспитательного процесса в их единстве позволяет заинтересовать и вовлечь детей в систему дополнительного образования. Разнообразие форм даёт возможность увеличить число воспитывающих факторов, влияющих на сознани ...
Причины неуспеваемости учащихся по химии в средней школе
Психологические исследования последних лет позволяют учителю-предметнику получить весьма важные сведения о типичных возрастных особенностях сформированности у учащихся определенного возраста различных интеллектуальных умений и других качеств личности. Эти сведения, к сожалению, не стали исходной ос ...
Задачи физического
воспитания детей старшего дошкольного возраста в условиях ДОУ
Основной задачей физического воспитания, как и воспитания вообще в ДОУ, является формирование здорового, всесторонне развитого ребенка. Система работы в МДОУ "Колокольчик" предусматривает обязательное планомерное и систематическое воздействие на ребенка средствами физического воспитания. ...