Геометрия на спичках

В работе над задачками можно использовать спички, счётные палочки или просто рисунок на бумаге. Спички имеют стандартную длину и это свойство позволяет строить из них различные геометрические фигуры. Одна спичка - это модель отрезка.

Данное занятие целесообразно провести в форме викторины. Разделить участников кружка на команды (желательно на 2 команды, а также несколько человек сделать независимым жюри). Дать учащимся время на выбор в каждой команде капитана, название команды. По окончании игры можно подарить каждой команде сувениры, приготовленные заранее.

В начале занятия учитель сообщает учащимся, что он - телепат, и может угадать трехзначное число, которое любой из учащихся загадает.

Учитель (обращаясь к одному из участников кружка):

Возьми бумажку. Запиши на ней трехзначное число. Мне не показывай!

Припиши к нему это же число еще раз.

Теперь передай своему соседу.

Теперь второй учащийся должен разделить это число на 7 и передать бумажку дальше.

Следующий нам разделит это число на 11, запишет его на чистой бумажке и отдаст результат учителю.

Слушаем ответ! Правильно? Конечно правильно, это и называется телепатия.

Секрет: последний результат надо разделить на 13 и мы получим исходное число.

Разъяснение: Когда мы к трехзначному числу приписали такое же число, то мы тем самым умножили его на 1001, а затем, разделив последовательно на 7, 11, 13, мы разделили его на 1001, то есть получили задуманное трехзначное число.

Далее учитель может предложить одному из учащихся загадать число от 1 до 12, и сказать, что это число может быть угадано. На доске заранее вывешен круг, на котором изображены числа от 1 до 12, (для той же цели можно взять часы и предложить угадать кем-либо час).

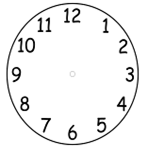
Учитель:

просит загадать любого участника кружка одно из чисел, изображенных на кругу и не говорить его.

Сам выбирает произвольное число n (также из круга).

Указывает его ученику.

Предлагает продолжить счет от задуманного учеником числа против часовой стрелки, стартуя с числа, указанного учителем и закончив на числе n+12.

Когда же учащийся досчитает, то как раз сам укажет на задуманное им число.

"Угадать возраст"

Предложить умножить человеку, у которого пытаемся узнать возраст, число лет на 2, прибавить 5, а сумму снова умножить на 5. Полученное число сообщить.

Секрет фокуса: Нетрудно догадаться, что последней цифрой результата будет цифра 5. Ее необходимо отбросить а от оставшегося числа отнять 2. Разность и есть искомый результат.

"Угадывание дня, месяца и года рождения"

Предложить одному из учащихся выполнить следующие действия: “Умножить номер месяца, в котором он родились, на 100, затем прибавить день рождения, результат умножить на 2, к полученному числу прибавить 2, результат умножить на 5, к полученному числу прибавить 1, к результату приписать 0, к полученному числу прибавить еще 1 и, наконец, прибавьте число его лет. После этого он должен сообщить, какое число у него получилось.

Секрет фокуса: от названного числа отнять 111, а потом остаток разбить на три грани справа налево по две цифры. Средние две цифры обозначают день рождения, первые две или одна - номер месяца, а последние две цифры - число лет, зная число лет, определяется год рождения.

Фокусы с предметами.

"День недели"

Необходимо заранее подготовить семь табличек, на которых написаны и пронумерованы дни недели, и предложить каждому выбрать любой один день. Затем отвернуться от зрителей, а те, выбрав по таблице, положат их на стол надписями вниз.

Далее по команде каждый увеличивает порядковый номер выбранного дня в два раза, к этому произведению прибавляет 5, затем полученную сумму умножает на 5, а то, что получается, умножает на 10. По объявленному каждым зрителем результату называется выбранный день. Подтверждая правильность ответов, зрители поочередно демонстрируют всем свою таблицу.

Секрет фокуса: Из первой (левой) цифры каждого объявленного результата вычитается 2. Остаток указывает номер выбранного дня недели.

Разъяснение: После первого и второго действия, разность между числами составляет 2. После третьего - 10. Тем самым мы пришли к тому, что разряд десятков идет по порядку, начиная с 3. Вычитая 2 из числа разрядов, мы приходим к исходным данным. Последнее действие, умножение на 10, не столь важно, можно обойтись и без него. Оно служит лишь для того, чтобы запутать зрителей. Можно составить таблицу результатов всех действий.

Актуально о образовании:

Советская школа до начала 30-х гг
Уже в конце 1917 г. начала проводиться национализация всех типов учебных заведений. Школа была объявлена не только единой и трудовой, но и бесплатной, общеобязательной и общедоступной. Была заявлена преемственность ступеней образования, обеспечивалось равенство возможностей образования. Была осущес ...

Экспериментальная работа по обучению рассказыванию
Давно установлено, что к старшему дошкольному возрасту проявляются существенные различия в уровне развития речи детей. Это показывает и наш опыт педагогической деятельности. Главной задачей развития связной речи ребёнка в данном возрасте является совершенствование монологической речи. Эта задача ре ...

Анализ средств развития мелкой моторики детей с нарушением интеллекта
нарушение интеллект моторика лечебный Одной из основных причин, затрудняющих формирование у детей с нарушением интеллекта двигательных умений и навыков, являются нарушения моторики, которые в свою очередь отрицательно сказываются не только на физическом развитии, но и на социализации личности, разв ...