Графы. Применение графов к решению задач

Графы - это рисунки, которые состоят из точек и линий, соединяющих эти точки.

Каждая пара точек в графе может быть соединена линиями. Линия указывает на связь между двумя точками. Точки называются вершинами графа, а линии - рёбрами.

С какими графами вы встречаетесь повседневной в жизни? (схемы авиалиний, которые часто вывешивается в аэропортах, схемы метро, а на географических картах - изображение железных дорог). С помощью графов изображаются схемы дорог, газопроводов, тепло и электросетей.

Особым видом графа является дерево. Дерево (граф) - это способ организации информации об отношениях между объектами, в нем нет циклов, то есть нельзя из некоторой вершины пройти по нескольким различным ребрам и вернуться в ту же вершину. Примером такого дерева может служить генеалогическое дерево Рюриковичей и Романовых.

Рассмотрим одну из простейших задач: Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля - Меркурий; Плутон - Венера; Земля - Плутон; Плутон - Меркурий; Меркурий - Венера; Уран - Нептун; Нептун - Сатурн; Сатурн - Юпитер; Юпитер - Марс и Марс - Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса?

Решение: Нарисуем схему условия: планеты изобразим точками, их у нас 9, а маршруты ракет - направляющими линиями.

Теперь сразу видно, что долететь с Земли до Марса нельзя.

Запишем еще одно определение: Степенью вершины графа называется количество выходящих из нее ребер. В связи с этим, вершина, имеющая четную степень, называется четной вершиной, соответственно, вершина, имеющая нечетную степень, называется нечетной вершиной.

1). В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими?

Решение: Допустим, что такое соединение телефонов возможно. Тогда представим себе граф, в котором вершины обозначают телефоны, а ребра - провода, их соединяющие. Подсчитаем, сколько всего получится проводов. К каждому телефону подключено ровно 5 проводов, т.е. степень каждой вершины нашего графа - 5. Чтобы найти число проводов, надо просуммировать степени всех вершин графа и полученный результат разделить на 2 (т.к. каждый провод имеет два конца, то при суммировании степеней каждый провод будет взят 2 раза). Но тогда количество проводов получится разным15·5/2=37,5. Но это число не целое. Значит наше предположение о том, что можно соединить каждый телефон ровно с пятью другими, оказалось неверным.

Ответ. Соединить телефоны таким образом невозможно.

2). В государстве 100 городов к из каждого города выходит 4 дороги. Сколько всего дорог в государстве.

Решение. Подсчитаем общее количество выходящих городов дорог - 100.4 = 400. Однако при таком подсчете каждая дорога посчитана 2 раза - она выходит из одного города и входит в другой. Значит всего дорог в два раза меньше, т.е. 200.

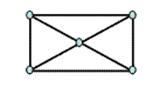
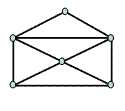
3). Обрисовать фигуру, не отрывая карандаша от бумаги и не проводя два раза по одной линии. Обозначьте точки пересечения, в скобках укажите, сколько линий выходит из данной точки. Если число линий четное - то вершина четная, если число линий нечетное - то вершина нечетная. Пометить вершину, с которой надо начинать обход.

1. 2. 3.

Актуально о образовании:

Общие методические рекомендации начинающему педагогу по проектированию увлекательных уроков
Если ты молодой педагог и хочешь, чтобы твои уроки были увлекательными, пробуждали познавательный интерес, то необходимо помнить следующие положения и действовать в соответствии с ними: Увлеченность педагога и поиск деятельности, в которой он может полностью реализовать себя, творчески самораскрыть ...

Модернизация образования
За последние десять лет система российского образования претерпела значительные изменения в русле общих процессов демократизации жизни общества, формирования рыночной экономики. Это стало возможным в результате последовательной реализации законодательных актов в области образования, других норматив ...

Международной конференции «Планетарий XXI века»
6–7 апреля 2012 года в МАУ города Ярославля «Культурно-просветительский центр имени В. В. Терешковой» состоялась Международная конференция «Планетарий XXI века». В конференции приняли участие работники планетариев России, Белоруссии, Казахстана, Германии, лётчики-космонавты, учёные. Конференция при ...