Ориентированный процесс случайного блуждания как метод прогнозирования

Случайная величина распределена нормально с параметрами

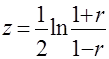; (7)

,

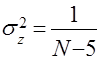где – значение выборочного коэффициента корреляции, определяемое по зависимости (4.5).

Моделируем значения как нормально распределенную случайную величину по зависимости

, (4.8)

где – нормированная нормально распределенная случайная величина, моделируемая с помощью алгоритма.

Осуществляя обратный по отношению к преобразованию Фишера переход, получим случайное значение коэффициента корреляции

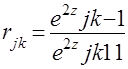. (4.9)

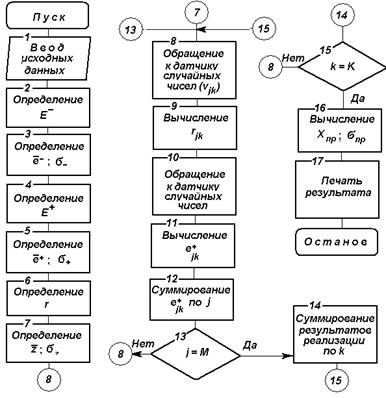
Рис. 4.3. Блок-схема алгоритма прогнозирования с использованием ориентированного процесса случайного блуждания

С учетом изложенного моделирование приращений на периоде упреждения включает выполнение следующих действий:

обращение к датчику нормированных нормально распределенных случайных чисел и получение ;

вычисление случайного значения по зависимостям (4.8) и (4.9);

обращение к датчику равномерно распределенных случайных чисел и получение числа ;

вычисление приращения по зависимости (4.6) при полученном в п. 2 значении коэффициента корреляции , определенном в п. 3 значении .

Многократно имитируя приращения и используя зависимости (4.1) и (4.2), вычисляются характеристики прогноза. Блок-схема алгоритма изображена на рис.4.3.

К достоинствам рассмотренного метода прогнозирования относятся:

простота вычислительного алгоритма;

возможность использования при ограниченной на периоде основания информации (начиная с 7-9 значений динамического ряда);

простота оценивания точности прогноза (определения дисперсии).

Актуально о образовании:

Образовательная реформа конца 80-х - начала 90-х гг
В 1988 году при Госкомитете был создан Временный научно-исследовательский коллектив (ВНИК). В него вошли и сотрудничали с ним многие думающие педагоги и психологи страны. Целью создания ВНИКа была разработка принципиально новой образовательной политики, основанной на идеях развития личности школьни ...

Сущность, задачи и содержание физического воспитания
В культуре и педагогике разных народов физическое развитие и воспитание всегда занимало важное место. Известны древневосточные и античные учения о гармоническом развитие человека, где физическое совершенство рассматривалось в единстве с умственным и нравственным. Физическое воспитание в европейских ...

Цели место и изучения физики в общеобразовательной школе
Среди основных целей общеобразовательной школы особенно важными являются две: передача накопленного человечеством опыта в познании мира новым поколениям и оптимальное развитие всех потенциальных способностей каждой личности Таким образом, можно выделить следующие задачи обучения физике в школе: фор ...