Ориентированный процесс случайного блуждания как метод прогнозирования

Как видно из изложенного, процедура определения характеристик прогноза при предлагаемом подходе отличается простотой, но вместе с тем характеризуется некоторой громоздкостью, обусловленной применением метода статистических испытаний. Поэтому коренным вопросом является рациональное моделирование приращений.

При наличии динамических рядов, имеющих продолжительный период основания, позволяющий получить репрезентативную выборку приращений, моделирование можно осуществлять в соответствии с определенным по этой выборке эмпирическим законом распределения приращений.

Для коротких динамических рядов можно применить допущение о нормальности отклонений значений динамического ряда от тренда. При этом допущении плотность распределения приращений также является нормальной.

При наличии на периоде основания информации малого объема (короткие динамические ряды) для моделирования приращений целесообразно использовать двумерное нормальное распределение. Двумерная плотность вероятности зависит в этом случае от пяти параметров:

,

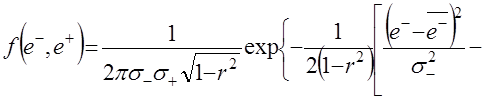
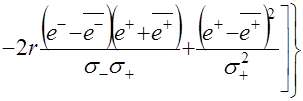где – случайные значения, математические ожидания и среднеквадратические отклонения предыдущих и последующих приращений переменной объекта прогнозирования соответственно; – коэффициент корреляции последующих приращений на предыдущие.

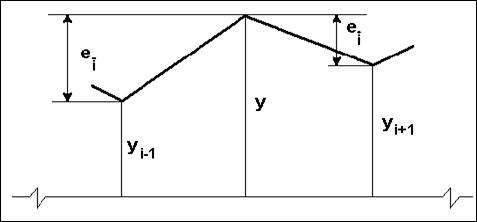
Рис. 4.2 График определения предыдущих и последующих приращений

Графически определение предыдущих и последующих приращений показано на рис. 4.2.

Очевидно, что одно и то же приращение в зависимости от того, относительно какой точки оно рассматривается, может быть как предыдущим, так и последующим. Однако первое приращение является только предыдущим.

При обработке исходного динамического ряда определяются оценки математических ожиданий и дисперсий предыдущих и последующих приращений. Множество предыдущих приращений определяется по зависимости

.

Множество последующих приращений определяется по зависимости

или

.

По множеству определяются среднее значение и оценка дисперсии предыдущих приращений:

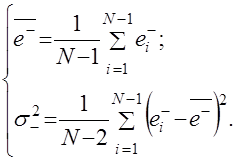(4.3)

Соответственно, по множеству определяются среднее значение и оценки дисперсии последующих приращений:

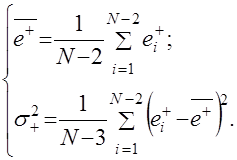(4.4)

Оценка значения коэффициента корреляции определится по зависимости

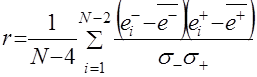. (4.5)

Для моделирования случайных приращений на периоде упреждения используется алгоритм моделирования двумерного нормального распределения. Для рассматриваемого случая моделирующая зависимость последующих приращений имеет вид

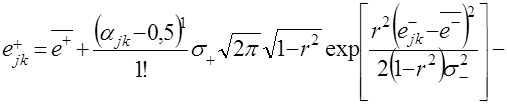
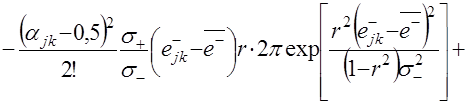
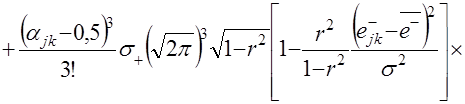
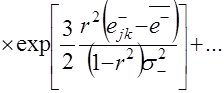(4.6)

При моделировании случайного значения на первом шаге в каждой -й реализации предыдущее значение равно значению последнего приращения на периоде основания ,то есть

При моделировании приращений на следующих шагах периода упреждения

.

Оценка коэффициента корреляции, определяемая по выборкам малых объемов, является случайной. Плотность вероятности выборочного коэффициента корреляции имеет сложный вид. При принятом допущении о нормальности распределения приращений используется нормализующее преобразование Фишера.

Актуально о образовании:

Размышления рядового учителя по вопросу содержания современного образования
Полностью согласна с учеными, поставившими на первое место образования, - духовно-нравственное воспитание ребенка. Все остальное приложится. К сожалению, современный учитель поставлен в такие рамки, из которых «выбраться» подчас просто невозможно. Ведь предметник обязан подготовить детей к ЕГЭ, а з ...

Выявление меры связи между характеристиками мышления и успешностью в обучении математике
После проведения исследований характеристик мышления и получения результатов проверим гипотезу о связи между мышлением учеников и их достижениями в математике. Попробуем установить, влияет ли уровень развития мышления учащихся на их успешность в обучении математике, зависят ли результаты обучения о ...

Ознакомление детей 7 лет с немецкой культурой
1. развитие коммуникативных навыков у детей, творческой активности и самостоятельности. 2. расширение представлений о культуре, традициях, праздниках в Германии. 3. развитие творческих, художественных, актёрских способностей. 4. вызвать у детей желание участвовать в коллективной деятельности. Работ ...