Ориентированный процесс случайного блуждания как метод прогнозирования

Применение аналитических и статистических моделей связано с априорным поиском структуры этих моделей чаще всего при ограниченной информации о характере развития процесса. Определение параметров статистической модели и оценка точности прогноза требуют к тому же наличия необходимых статистических данных, характеризующих поведение объекта на периоде основания прогноза. Указанные обстоятельства в первую очередь снижают достоверность выводов в задачах прогнозирования развития технических систем.

Для выполнения прогноза предлагается подход, не связанный с использованием жесткой структуры модели и серьезными требованиями к объему априорной информации. Сущность метода заключается в представлении используемого для прогнозирования динамического ряда в качестве определенным образом ориентированного процесса случайного блуждания.

Значение изменяющегося параметра объекта прогнозирования для каждого момента на периоде основания можно представить в виде

,

где – значение динамического ряда в -й момент времени (год) периода основания;

– значение динамического ряда в предыдущий момент времени;

– приращение переменной объекта прогнозирования в -й момент времени по сравнению с предыдущими;

– число значений динамического ряда.

Поскольку приращения носят случайный характер, для них можно определить вид закона распределения и его параметры. При этом нужно учесть характер зависимости последующих приращений от предыдущих.

Предполагается, что в период упреждения характер изменения динамического ряда сохраняется. Тогда, используя характеристики приращений, метод статистических испытаний можно применить для моделирования приращений в период упреждения прогноза. Значение единичной реализации прогноза на каждом последующем шаге прогнозирования будет

,

где – номер шага на периоде упреждения;

– число шагов на периоде упреждения;

– значение переменной объекта прогнозирования на предыдущем шаге;

– моделируемое значение приращения на -м шаге.

Производя данную процедуру до момента прогнозирования, получим значение точечного прогноза

,

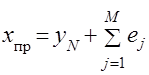где – точечный прогноз на -й период упреждения;

– конечное значение динамического ряда.

При разыгрывании данной процедуры многократно образуется совокупность случайных значений точечного прогноза. По полученной выборке значений определяются среднее значение прогноза и его дисперсия:

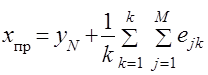; (4.1)

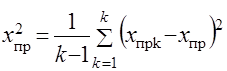, (4.2)

где – число реализаций точечного прогноза;

– разыгрываемое значение приращения на -м шаге периода упреждения в -й реализации точечного прогноза;

– значение -й реализации точечного прогноза, определяемое по зависимости (1).

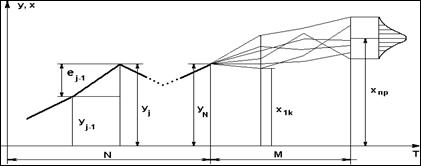
Рис. 4.1 Графическое отображение процесса случайного блуждания

Таким образом, процедура прогнозирования сводится к многократной имитации приращений на периоде упреждения и последующему определению статистических характеристик (среднего и дисперсии) реализаций точечного прогноза. График предлагаемого метода показан на рис. 4.1.

Актуально о образовании:

Установка и внимание в обучении
В отечественной педагогике утвердилось положение о том, что развитие личности в процессе обучения зависит как от внешних, так и от внутренних условий. К внешним условиям относятся педагогическое мастерство учителя (преподавателя); рациональное построение учебных программ, учебников, учебных пособий ...

Периодизация с точки зрения ведущих видов деятельности
Осознание значимости детства в процессе становления личности приходит довольно поздно. Открытие личности в эпоху Возрождения лишь спустя два столетия приводит к поискам ее истоков, к постановке проблемы ее формирования и развития. Новая наука - детская психология появляется в конце XIX столетия, и ...

Анализ программы Конышевой Н.М. «Методика трудового обучения младших школьников: основы дизайнообразования»
Прежде чем перейти непосредственно к раскрытию некоторых методических аспектов в изучении народной культуры, на наш взгляд, следует сказать с существующих ныне новых программах трудового обучения. Их много, но, по нашему мнению, наибольшего внимания заслуживает программа трудового обучения (основам ...