Круги Эйлера

Примерное содержание сообщения учащегося о Леонарде Эйлере.

Рассказ учителя о кругах Эйлера.

Очень часто бывает так, что решение задачи помогает найти рисунок. Использование рисунка делает решение задачи простым и наглядным.

Рассмотрим такую задачу.

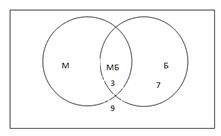
1). В классе 35 учеников. Из них: 19 ребят занимают в математическом кружке, 10 - в биологическом, 9 ребят не посещают эти кружки. Сколько биологов увлекаются математикой?

Решение. Для решения задачи изобразим в виде "кругов" учащихся,

занимающихся математикой и биологией.

Обозначим их буквами М и Б соответственно. Круги М и Б содержатся в прямоугольнике, которым мы изображаем всех учащихся класса.

Нам очевидно, что общая часть кругов М и Б состоит из тех ребят, которые одновременно увлекаются и математикой, и биологией. Теперь давайте посчитаем. Всего внутри прямоугольника 35 ребят. Внутри двух маленьких кругов М и Б будет 35-9= 26 ребят, поскольку нам известно, что 9 ребят не посещают кружки. Внутри "математического" круга 19 ребят, значит, в той части "биологического" круга, которая расположена вне круга М, находится 26-19= 7 биологов, не посещающих математический кружок. Остальные биологи, их 10-7= 3, находятся в общей части кругов МБ. Таким образом, 3 биолога увлекаются математикой.

Изображение различных множеств в виде кругов широко использовал в своих научных трудах великий математик ХVIII века Леонард Эйлер. Именно поэтому рисунки, подобные в задаче, которую разобрали выше, обычно называют "кругами Эйлера". Эйлер отмечал, что изображение множеств в виде кругов "очень подходит для того, чтобы облегчить наши рассуждения".

Круги Эйлера - геометрическая схема, с помощью которой можно изобразить отношения между подмножествами.

2). В киоске около школы продается мороженое двух видов: "Спортивное" и "Мальвина". На перемене 24 ученика успели купить мороженое. При этом 15 из них купили "Спортивное", а 17 - мороженое "Мальвина". Сколько человек купили мороженое обоих сортов?

Решение. Попробуем изобразить данные задачи с помощью кругов.

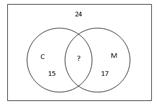
Общая часть кругов состоит из тех школьников, которые купили мороженое обоих сортов. Всего мороженое купили 24 ученика. Внутри круга М 17 учеников, а в круге С - 15 учеников. Возьмем, например, учащихся, купивших мороженое "Мальвина". Получим 24-17=7 учащихся, которые купили мороженое "Спортивное", но не купили мороженое "Мальвина". Остальные учащиеся: 15-7= 5 купили и мороженое "Спортивное", и "Мальвина". Таким образом, мы получили 5 учеников, которые купили оба вида мороженого.

3). Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским - 28, французским - 42. Английским и немецким одновременно владеют 8 человек, английским и французским - 10, немецким и французским - 5, всеми тремя языками - 3. Сколько туристов не владеют ни одним языком?

Актуально о образовании:

Графы. Применение графов к решению задач
Графы - это рисунки, которые состоят из точек и линий, соединяющих эти точки. Каждая пара точек в графе может быть соединена линиями. Линия указывает на связь между двумя точками. Точки называются вершинами графа, а линии - рёбрами. С какими графами вы встречаетесь повседневной в жизни? (схемы авиа ...

Выявление связи между уровнем понятийного мышления учащихся и их учебными достижениями по математике
Применим метод ранговой корреляции Спирмена для нашего исследования. Перед подсчетом коэффициента корреляции убедимся, что между уровнем понятийного мышления учащихся и их учебными достижениями по математике существует определенная связь. Для этого по рангам, полученным учениками, построим диаграмм ...

Педагогические условия развития связной речи
В философском словаре условие рассматривается как «категория», выражающая отношение предмета к окружающим его явлениям, без которых этот предмет существовать не сможет. Сам предмет выступает как нечто обусловленное, а условие – как относительно внешнее предмету многообразие объективного мира. Услов ...