Графы. Применение графов к решению задач

4.

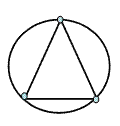
Все ли фигуры у вас получилось нарисовать? (все, кроме фигуры №1). Как вы думаете почему? Как это связано с количеством четных и нечетных вершин?

Сделаем вывод:

Если все вершины графа четные, то нарисовать фигуру возможно, и начать можно с любой вершины (№4).

Если же из этих вершин две нечетные, то нарисовать фигуру можно, но только начинать необходимо в одной из этих двух нечетных вершин, а заканчивать во второй нечетной вершине (№2, №3).

Если в графе более двух нечетных вершин, то нарисовать фигуру невозможно (№1).

Вопрос о разрешимости таких задач входит в теорию графов. Впервые ее исследовал Л. Эйлер в 1736г., решая задачу о Кенигсбергских мостах.

4). Город Кенигсберг расположен на берегах и двух островах реки Преголя. Части города соединены между собой семью мостами. В воскресные дни горожане совершили прогулки по городу. И возник вопрос, можно ли выбрать такой маршрут, чтобы пройти по каждому мосту только один раз и вернуться в начальную точку пути?

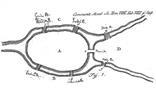
Попробуем разрешить эту задачу. Но сначала составим план города, как это сделал Л. Эйлер. Он обозначил части города точками (вершины), а переходы по мостам - линиями (ребра). Получил граф.

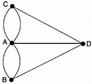
Ответ: обход по всем мостам только один раз невозможен, т.к. все вершины графа нечетные.

Поэтому графы, которые можно нарисовать указанным способом, называются Эйлеровыми графами.

Задачи для самостоятельного решения:

1). Алина решила маме на день рождения подарить букет цветов (розы, тюльпаны или гвоздики) и поставить их или в вазу или в кувшин. Сколькими способами это можно сделать?

2). Ранним утром Миша Маша, Андрей обменялись приветствиями каждый с каждым. Сколько всего было приветствий. Решите задачу с помощью графа. Нарисуй граф в рабочей тетради.

3). В квартирах №1,2,3 жили три друга: Айдар, Тима и Саша. Известно, что в квартирах №1 и 2 жил не Айдар. Тима жил не в квартире №1. В какой квартире жил каждый из друзей.

4). Может ли в государстве, в котором из каждого города выходит ровно 3 дороги, быть ровно 100 дорог?

5). Какие буквы русского алфавита можно нарисовать одним росчерком?

6). Муха забралась в банку из-под сахара. Банка имеет форму куба. Сможет ли муха последовательно обойти все 12 ребер куба, не проходя дважды по одному ребру. Подпрыгивать и перелетать с места на место не разрешается.

Актуально о образовании:

Изучение уровня самостоятельности учащихся 1 класса
Проблема самостоятельной деятельности младшего школьника имеет свою богатую историю в теоретическом освещении и реализации ее основных положений в практике работы школы. На этой основе мы спланировали и провели эксперимент, который проходил на базе ГУО "Ордатский УПК д-с СШ Шкловского района с ...

Интеллектуальные нарушения, причины нарушений интеллектуального развития у детей
Нарушение интеллекта у детей (умственная отсталость) – это стойкое, необратимое нарушение познавательной деятельности, вызванное органическим поражением головного мозга. Именно эти признаки: стойкость, необратимость дефекта и его органическое происхождение должны в первую очередь учитываться при ди ...

Условия эффективной организации художественно-творческой деятельности
Определение условий эффективной организации художественно-творческой деятельности детей относится к числу проблем, постоянно вызывающих интерес исследователей и поэтому довольно часто рассматривается в специальной литературе. Само понятие «условия» определяется как «обстоятельство, от которого что- ...