Задачи на совместную работу

При решении этих задач нужно выяснить с учащимися, что возможны два случая:

объем выполненной работы известен;

объем выполненной работы неизвестен.

Первые задачи удобно решать, используя таблицы.

Пример. Два токаря вместе изготовили 350 деталей. Первый токарь делал в день 40 деталей и работал 5 дней, второй работал на 2 дня меньше. Сколько деталей в день делал второй токарь?

Составим таблицу (см. табл.3).

Таблица 3

Условие задачи

Объяснение. Так как известны производительность и время работы первого токаря, найдем количество деталей, изготовленных первым токарем.

40*5 = 200 (дет.) – изготовил первый токарь.

Работая с таблицей, делаем вывод, что можно найти, сколько деталей изготовил второй токарь.

350 – 200 = 150 (дет.) – изготовил второй токарь.

Обратив внимание на опорные слова «на…меньше», делаем вывод, что можно найти, сколько дней работал второй.

5 – 2 = 3 (дня) – работал второй токарь.

Зная количество и время работы второго токаря, находим его производительность:

150 / 3 = 50 (дет.) – изготовлял второй токарь в день.

Уже при решении первых задач, нужно приучать детей к правильной терминологии.

Для решения задач второго типа, текст задачи можно проиллюстрировать чертежами, что помогает учащимся зрительно видеть задачу.

Пример 1. Новая машина может выкопать канаву за 8 часов, а старая – за 12. Новая работала 3 часа, а старая - 5 часов. Какую часть канавы осталось выкопать?

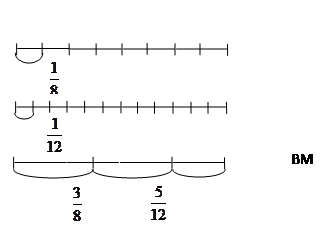
Рис.13. Графическое изображение задачи из примера №1

Дадим наглядное представление этих задач. Условимся, что объем выполненной работы неизвестен, поэтому принимаем его за 1 и изображаем в виде отрезка, но отрезков будет три, так как возможны три случая:

работает одна старая машина;

работает одна новая машина;

работают вместе обе машины.

Выясним, почему отрезки равной длины (обе машины выполняют одну и ту же работу).

Разбор задачи. На сколько равных частей делим первый отрезок? На 8, так как работа выполняется за 8 часов. Что показывает 1 часть? Какую часть работы выполняет новая машина за 1 час, т.е. какова ее производительность?

Так как новая машина работала 3 часа, то выполнила части все работы. Отмечаем на третьем отрезке - .

Аналогичные рассуждения проводим, рассматривая старую машину, и отмечаем на третьем отрезке - .

Далее рассматривается третий нижний отрезок, и по нему выясняется, как найти оставшуюся часть, т.е., отрезок, обозначенный знаком вопроса.

В связи с экономией времени деление отрезков производится «на глаз», хотя очень полезно показать, как можно разделить быстро на 4 равные части (отрезок делится пополам, а затем каждая часть еще пополам). Аналогично деление на 8 и т.д. На 6 частей – сначала пополам, а потом каждую часть - на три.

Пример №2. Два кузнеца, работая вместе, могут выполнить работу за 8 часов. За сколько часов может выполнить работу первый кузнец, если второй выполняет ее за 12 часов?

Актуально о образовании:

Сущность самостоятельности как интегративного качества личности
Самостоятельность - понятие, которое достаточно часто встречается на страницах публикаций, посвященных человеку. Им оперируют философы, общественные и государственные деятели, писатели, люди искусства, политики, социологи, а также психологи и педагоги. Практически в любой теории или концепции, каса ...

Закономерности воспитательного процесса
Воспитательный процесс, являясь частью целостного педагогического процесса, подчиняется его общим закономерностям, но, кроме того, имеет ряд специфических закономерностей Ведущей и основополагающей закономерностью личностно ориентированного воспитательного процесса можно считать следующую: Чем выра ...

Функции и структура системы среднего образования в РФ
Система образования в Российской Федерации представляет собой совокупность взаимодействующих: преемственных образовательных программ и государственных образовательных стандартов различного уровня и направленности; сети реализующих их образовательных учреждений независимо от их организационно-правов ...