Элементы комбинаторики. Принцип Дирихле

В начале занятия кратко рассказать историю зарождения комбинаторики и об областях ее применения.

Определение. Задачи на составление числа возможных соединений элементов с определенными свойствами, которые можно составить из элементов заданного множества, называются комбинаторными.

Задача 1. Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7?

Решение: Для того чтобы не пропустить и не повторить ни одно из чисел, будем выписывать их в порядке возрастания. Сначала запишем числа, начинающиеся с цифры 1, затем с цифры 4 и, наконец, с цифры 7. Получаем следующий расклад.

Таким образом, из трех данных цифр можно составить всего 9 различных двузначных чисел.

Данный метод называется методом перебора.

Однако существует другой подход к решению самых разных комбинаторных задач с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда название - дерево возможных вариантов.

Вернемся к задаче о составлении двузначных чисел из цифр 1, 4 и 7. Для ее решения можно построить специальную схему.

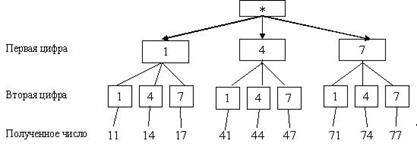
Эта схема действительно похожа на дерево, правда, "вверх ногами" и без ствола. Знак “*” изображает корень дерева, ветви дерева - различные варианты решения. Чтобы получить двузначное число, надо сначала выбрать первую его цифру, а для нее есть три варианта: 1, 4 или 7. Поэтому из точки * проведены три отрезка и на концах поставлены цифры 1, 4 и 7.

Теперь надо выбрать вторую цифру, а для этого также есть три варианта: 1, 4 или 7. Поэтому от каждой первой цифры проведено по три отрезка, на концах которых снова записано 1, 4 или 7. Итак, получено всего 9 различных двузначных чисел. Других двузначных чисел из этих трех цифр составить невозможно.

Дополнительная подзадача: Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7, если цифры десятков и единиц не повторяются?

Задача 2. Туристическая фирма планирует посещение туристами в Италии трех городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута?

Способ 1: Обозначим города их первыми буквами. Тогда код каждого маршрута будет состоять из трех букв: В, Р и Ф, каждая из которых должна быть использована только один раз, например, ВФР или ФРВ.

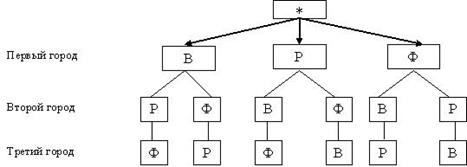
Варианты путешествия получаются следующие: ВРФ, ВФР, РВФ, РФВ, ФВР, ФРВ, что хорошо видно из дерева вариантов.

Путешествие можно начинать в любом из трех городов. Если первой посетить Венецию, то затем можно поехать в Рим или во Флоренцию. Если вторым посетить Рим, то третьей будет Флоренция, если второй будет Флоренция, то третьим будет Рим. Это первые два варианта путешествия. Таким образом, всего существует 6 вариантов путешествия.

Способ 2: Для каждого из трех городов существует 2 варианта маршрута по оставшимся городам. Если 3 умножить на 2, получится 6. Такой же ответ получится при помощи дерева вариантов.

Про второй способ рассуждений обычно говорят так: мы использовали правило умножения.

Комбинаторные задачи бывают самых разных видов. Но большинство из них решается с помощью двух основных правил - правила суммы и правила произведения. Продолжим знакомиться с правилом произведения (умножения), сформулируем утверждение: Если первую компоненту пары можно выбрать n способами, а вторую можно выбрать k способами, то число всевозможных комбинаций пар равно произведению чисел n и k.

Задача 3: Саша, Петя, Денис, Оля, Настя часто ходят в кафе. Каждый раз, обедая там, они рассаживаются по-разному. Сколько дней друзья смогут это сделать без повторения?

Решение: Пронумеруем стулья, на которых должен сесть каждый, и будем считать, что они рассаживаются поочередно:

№1 - Саша - есть возможность выбрать из 5 вариантов (стульев) №2 - Петя - 4 варианта №3 - Денис - 3 варианта №4 - Оля - 2 варианта №5 - Настя - 1 вариант

Используя правило умножения, получаем: 5х4х3х2х1=120

Теперь решим задачу, применяя правило сложения.

Задача 4: В коробке 6 синих карандашей и 12 красных. Сколько всего карандашей в коробке?

Актуально о образовании:

Индивидуальные особенности развития учащихся и их учет в процессе воспитания
Возрастные особен­ности развития учащихся по-разному проявляются в их индивидуальном формировании. Это связано с тем, что школьники в зависимости от природных задатков и ус­ловий жизни (связь биологического и социального) су­щественно отличаются друг от друга. Вот почему разви­тие каждого из них в ...

Выявление связи между уровнем концентрации внимания учащихся и их учебными достижениями по математике
Применим метод ранговой корреляции Спирмена для нашего исследования. Перед подсчетом коэффициента корреляции убедимся, что между уровнем концентрации внимания учащихся и их учебными достижениями по математике существует определенная связь. Для этого по рангам, полученным учениками, построим диаграм ...

Формирование самостоятельности у младших школьников
Целью формирующего этапа экспериментального исследования было с помощью специально подобранных форм, средств, путей и методов сформировать у младших школьников самостоятельность. Работа осуществлялась в несколько этапов. Основы методики воспитательной работы с младшими школьниками предполагают разу ...